The function $f (x) = x^{3} - 3 x$ is

A

increasing in $(- \infty, - 1) \cup (1, \infty)$ and decreasin in $(- 1, 1)$

B

increasing in $(0, \infty)$ and decreasingg in $(- \infty, 0)$

C

decreasing in $(0, \infty)$ and increasing in $(- \infty, 0)$

D

decreasing in $(- \infty, - 1) \cup (1, \infty)$ and increasingg in (-1,1)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We have, function $f (x) = x^{3} - 3 x$
$\Rightarrow f (x) = 3 x^{2} - 3 = 3 (x + 1) (x - 1)$

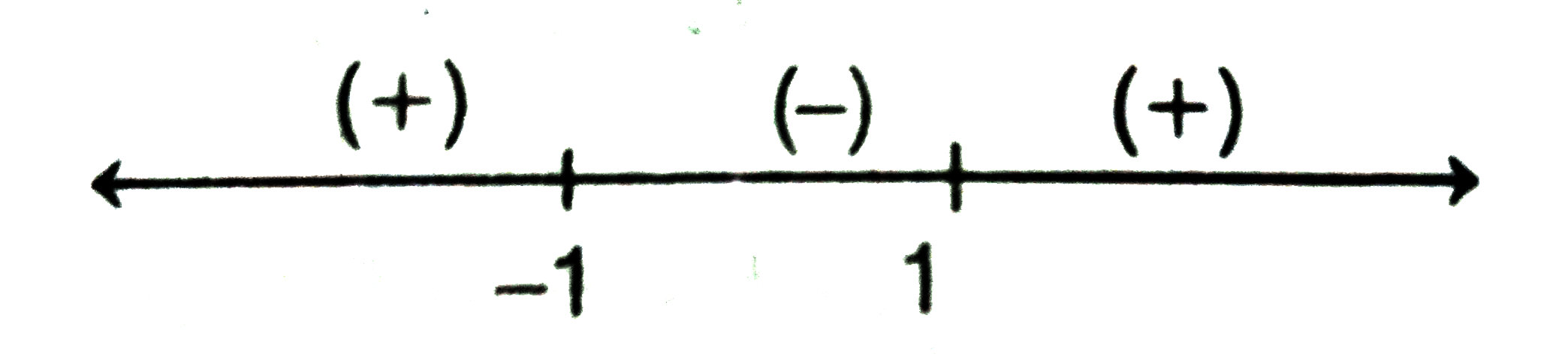
here, $f' (x) \geq 0$ in $(- \infty, - 1) \cup (1, \infty) and f' (x) < 0$ in (-1,1) $∴ f (x)$ is increasing $(- \infty, - 1), \cup (1, 00)$ and decreasing in (-1,1).

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the largest interval of x in which the function $f (x) = x^{3} - 3 x + 1$ is decreasing is (a, b), then the value of $a + 2 b$ is equal to
A $- 1$
B0
C1
D2
Question 2 - Select One
The value of $c$ in Rolle's theorem for the function $f (x) = x^{3} - 3 x$ in the interval $[0, \sqrt{3}]$ is
A $1$
B $- 1$
C $\frac{3}{2}$
D $\frac{1}{3}$
Question 3 - Select One
The value of $c$ in Rolle's theorem for the function $f (x) = x^{3} - 3 x$ in the interval $[0, \sqrt{3}]$ is
A $1$
B $- 1$
C $\frac{3}{2}$
D $\frac{1}{3}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-SOLVED PAPER 2019-MCQS

Home
Ask Doubt
Profile