Find the area of the region enclosed by the curve and the line y=2
Video Solution
Text Solution
Graph of the function is as shown in the following figure.
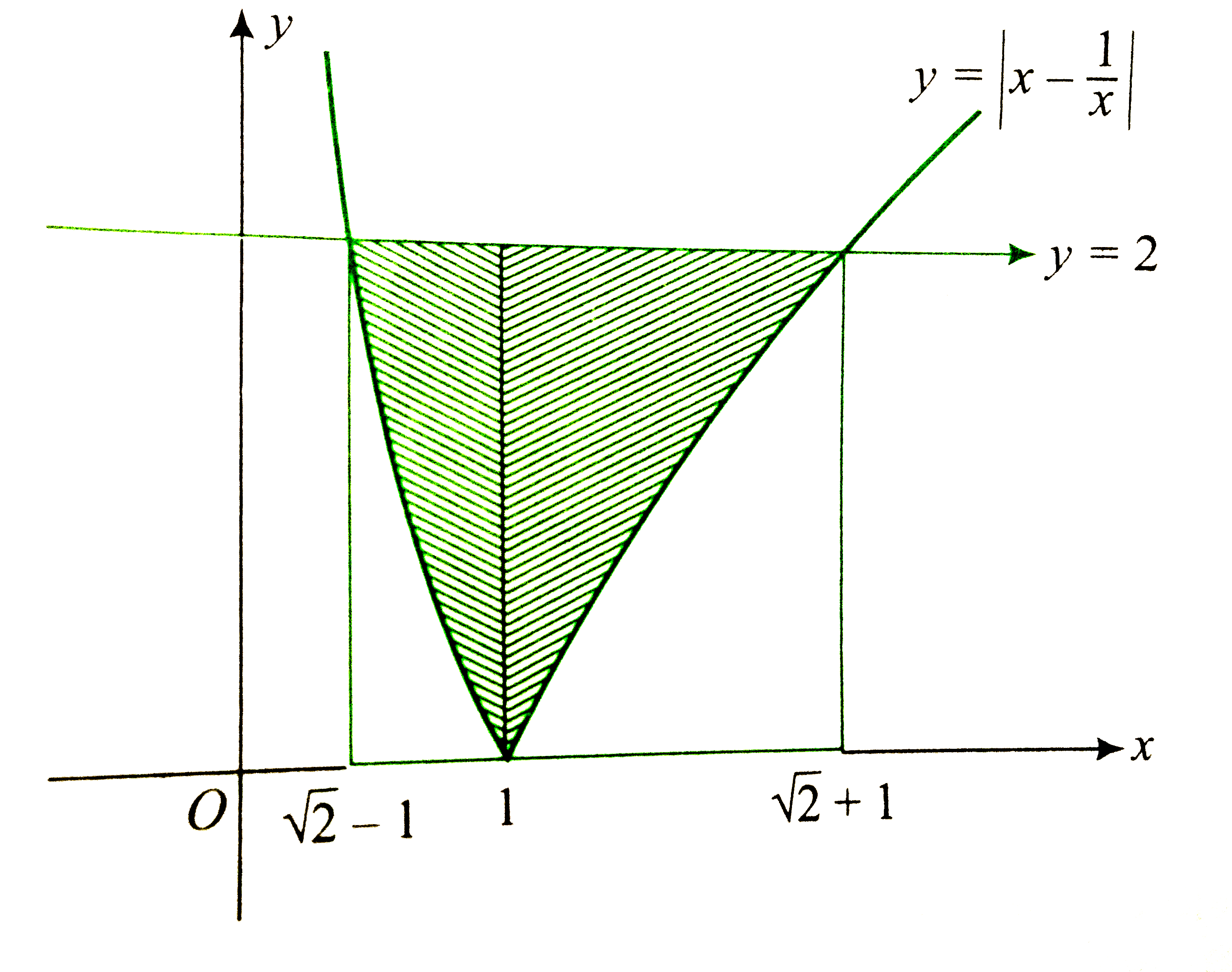
we get
we get
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.1
Explore 9 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.2
Explore 14 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
Let f(x)=x2/3,x≥0. Then the area of the region enclosed by the curve y=f(x) and the three lines y=x,x=1andx=8 is
A632B935C1057D12910The area of the region bounded by the curve C:y=x+1x2+1 nad the line y=1 , is
Aml −12In2+π4BIn2−π4+1C12In2+π4−1DIn 2−π2+1
Find the area of the region enclosed between curves y=|x−1| and y=3−|x|.
View SolutionFind the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
View SolutionFind the area of the region enclosed by the given curvesy=cosx,y=1−2xπ
View SolutionFind the area of the region enclosed by the curve y=x4–2x2andy=2x2.
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2;y=x;x=0 and x=3
View Solution
