Find the area bounded by the x-axis, part of the curve y=(1−8x2) , and the ordinates at x=2andx=4. If the ordinate at x=a divides the area into two equal parts, then find a.
A
√2 sq units
B
2√2 sq units
C
3√2 sq units
D
None of these
Video Solution
Text Solution
The correct Answer is:B
Area =∫42(1+8x2)dx
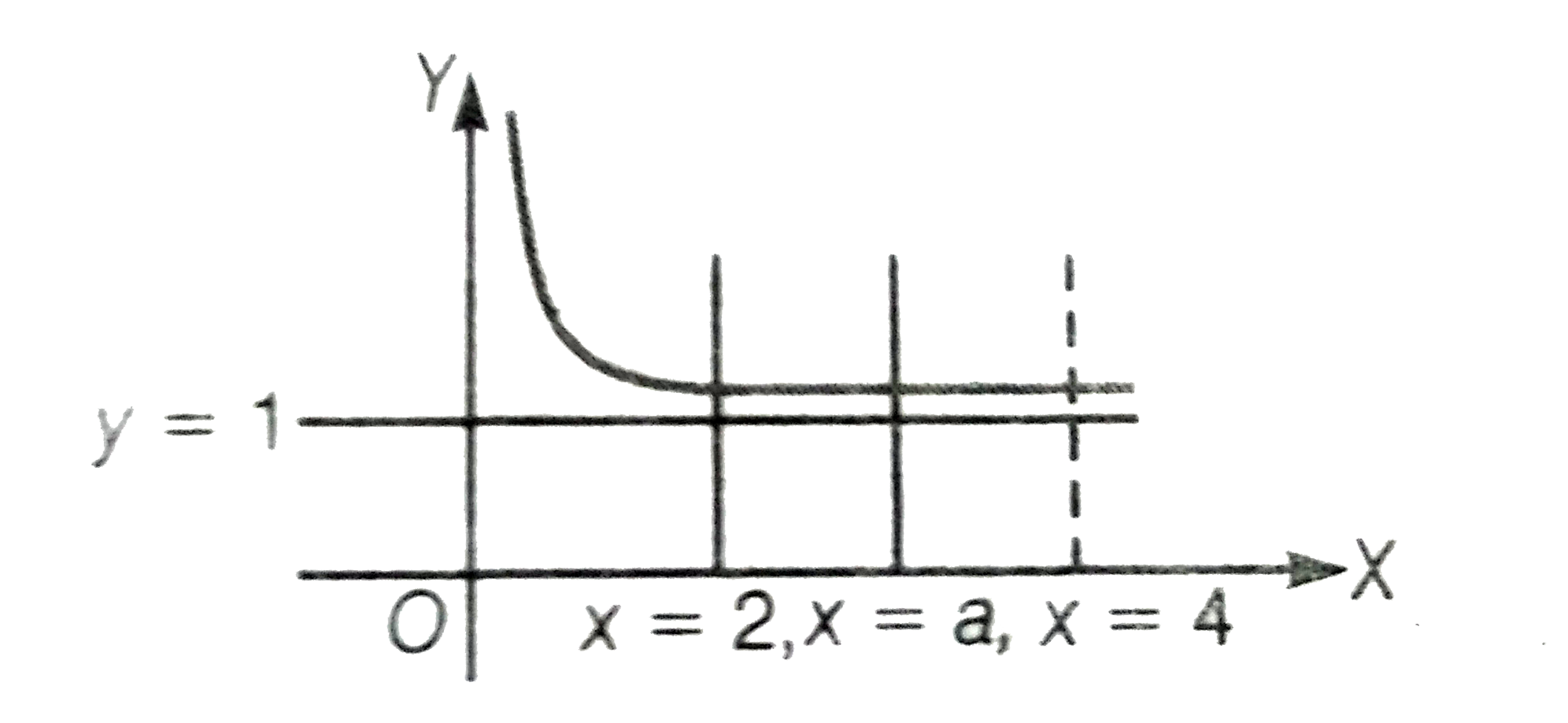
Since, the ordinate x = a divides area into two equal parts, therefore
∫a2(1+8x2)dx=12∫42(1+8x2)dx
⇒[x−8x]a2=12[x−8x]42
⇒(a−8a)−(2−4)=12[(4−2)−(2−4)]
⇒a−8a+2=2⇒a=√8=2√2 sq units
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MHT CET CORNER
Explore 21 Videos
Similar Questions
Knowledge Check
Let the area bounded by the x- axis, curve y=(1+8x2) and the ordinates x = 2 and x = 4 is "A" sq. unit and if the ordinate x = a divides the area into two equal parts, then the correct statement among the following is
AA = 3 and a = 2BA = 2 and a = 1CA=4√2 and a=√2DA=4 and a=2√2
The area bounded by the curve y=4x2 ,x-axis and the ordinates x=1,x=3 is
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionFind the area bounded by the curve |x|+y=1 and axis of x.
View SolutionFind the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionFind the area bounded by the curve y=xex2 , x-axis and the ordinates x=0 and x=h.
View Solution" The area bounded by the cure "y=1+(8)/(x^(2))" with "x" -axis and the ordinates "x=2" and "x=4" is "
View SolutionFind the area bounded by the curve y=logx, x-axis and the ordinates x=1&x=e.
View Solution

