The area bounded by the curves $y^{2} = 4 x$ and $x^{2} = 4 y$

A

0 sq units

B

$\frac{32}{3}$ sq units

C

$\frac{16}{3}$ sq units

D

$\frac{8}{3}$ sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

For the point of inersection for $y^{2} = 4 x and x^{2} = 4 y$

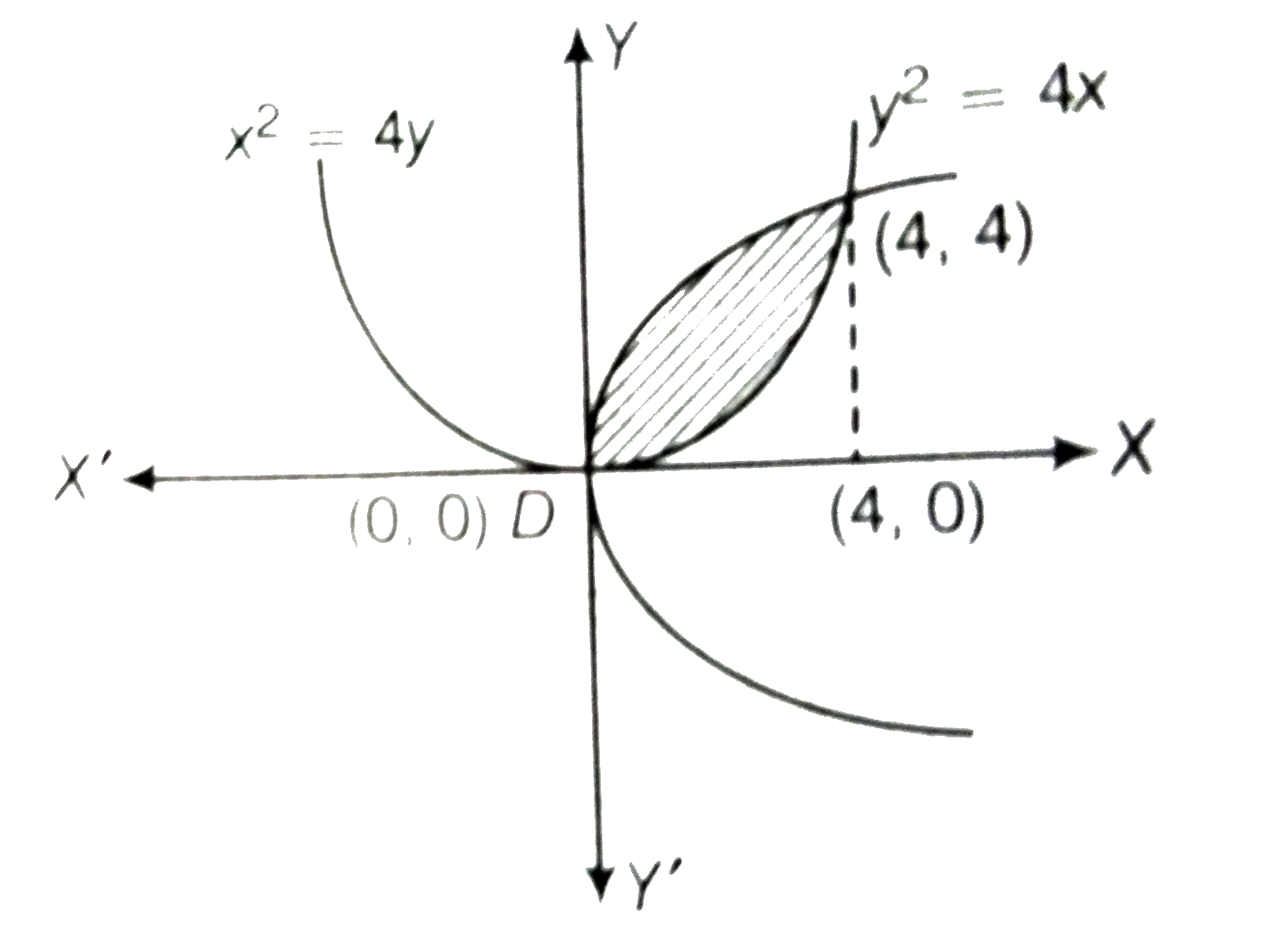
$\Rightarrow {(\frac{x^{2}}{4})}^{2} = 4 x$
$\Rightarrow x^{4} = 4^{3} x$
$\Rightarrow x = 0, 4$
$∴$ Area bounded between curves
$= \int_{0}^{4} (\sqrt{4 x} - \frac{x^{2}}{4}) d x = {⎡ ⎣ 2 . \frac{x^{3 / 2}}{\frac{3}{2}} - \frac{x^{3}}{12} ⎤ ⎦}_{0}^{4}$
$= \frac{4}{3} . {(4)}^{3 / 2} - \frac{{(4)}^{3}}{12} = \frac{32}{3} - \frac{16}{3} = \frac{16}{3}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these
Question 2 - Select One
The area bounded by the curves $y^{2} = x^{3} and | y | = 2 x$ is
A $\frac{5}{16}$ sq units
B $\frac{16}{5}$ sq units
C $\frac{3}{8}$ sq units
DNone of these
Question 3 - Select One
Find the area of the region bounded by the curve $y^{2} = 4 x and x^{2} = 4 y$ .
A $\frac{15}{7} sq units$
B $\frac{16}{7} sq units$
C $\frac{16}{3} sq units$
D $16 sq units$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -MHT CET Corner

Home
Ask Doubt
Profile