The area of the region bounded by the curves x2+y2=8andy2=2x (in sq. unit) is
A
2π+13
B
π+13
C
2π+43
D
π+43
Video Solution
Text Solution
The correct Answer is:C
Given curves x2+y2=8 ... (i)
and y2=2x ... (ii)
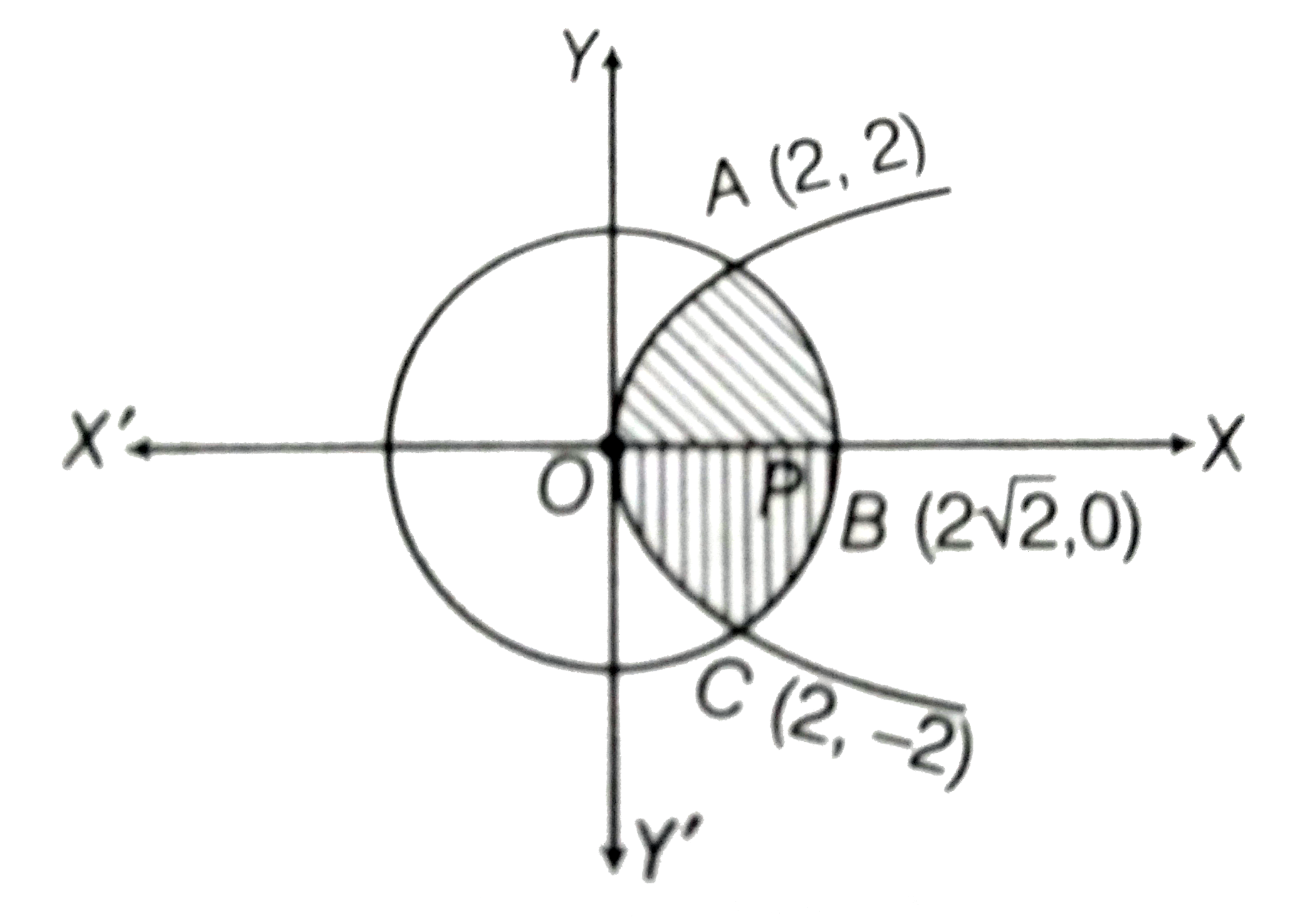
On solving Eqs. (i) and (ii), we get
x2+2x−8=0
x2+4x−2x−8=0
x(x+4)−2(x+4)=0
(x−2)(x+4)=0
∴ x = 2 and y=±2
∴ Required area = 2 [Area of OAP + Area of PAB]
2[∫20√2xdx+∫2/√22√8−x2dx]
=2⎡⎢⎣√2(x3/2.23)20+(x2√8−x2+82sin−1.x2√2)2√22⎤⎥⎦
=2[2√23.2√2+2π−2−π]
=2[83−2+π]=2(23+π)=2π+43
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:Exercise 2
Explore 34 Videos
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MHT CET CORNER
Explore 21 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the curves x=y2−2 and x=y is
A94B9C92D97The area of the region bounded by the curves y2=8x and y = x (in sq unit) is
A643B323C163D83The area of the region bounded by the curves x2+4y2=4 and 4y2=3x is
A(2π3+12√3) sq. unitB(3π2+22√3) sq. unitC(2π5+12√5) sq. unitDNone of these
Find the area of the region bounded by the curves 2y2=x,3y2=x+1,y=0.
View SolutionThe area of the region bounded by the curves y=x2 and x=y2 is
View SolutionThe area of the region bounded by the curve y=x2 and the line y=16 (in square units) is
View SolutionThe area of the region bounded by the curve y=x2 and y =|x| is equal to
View SolutionThe area of the region bounded by the curve y=x2 and y = x is equal to
View Solution