The optimal value of the objective function is attained at the points A)given by intersection of inequations with axes only B) given by intersection of inequations with X-axis only C) given by corner points of the feasible region D) none of teh above
given by intersection of inequations with axes only
given by intersection of inequations with X-axis only
given by corner points of the feasible region
None of the above
The correct Answer is:C
The optimal value of the objective function is attained at the points given by corner points of the feasible region.
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
The optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
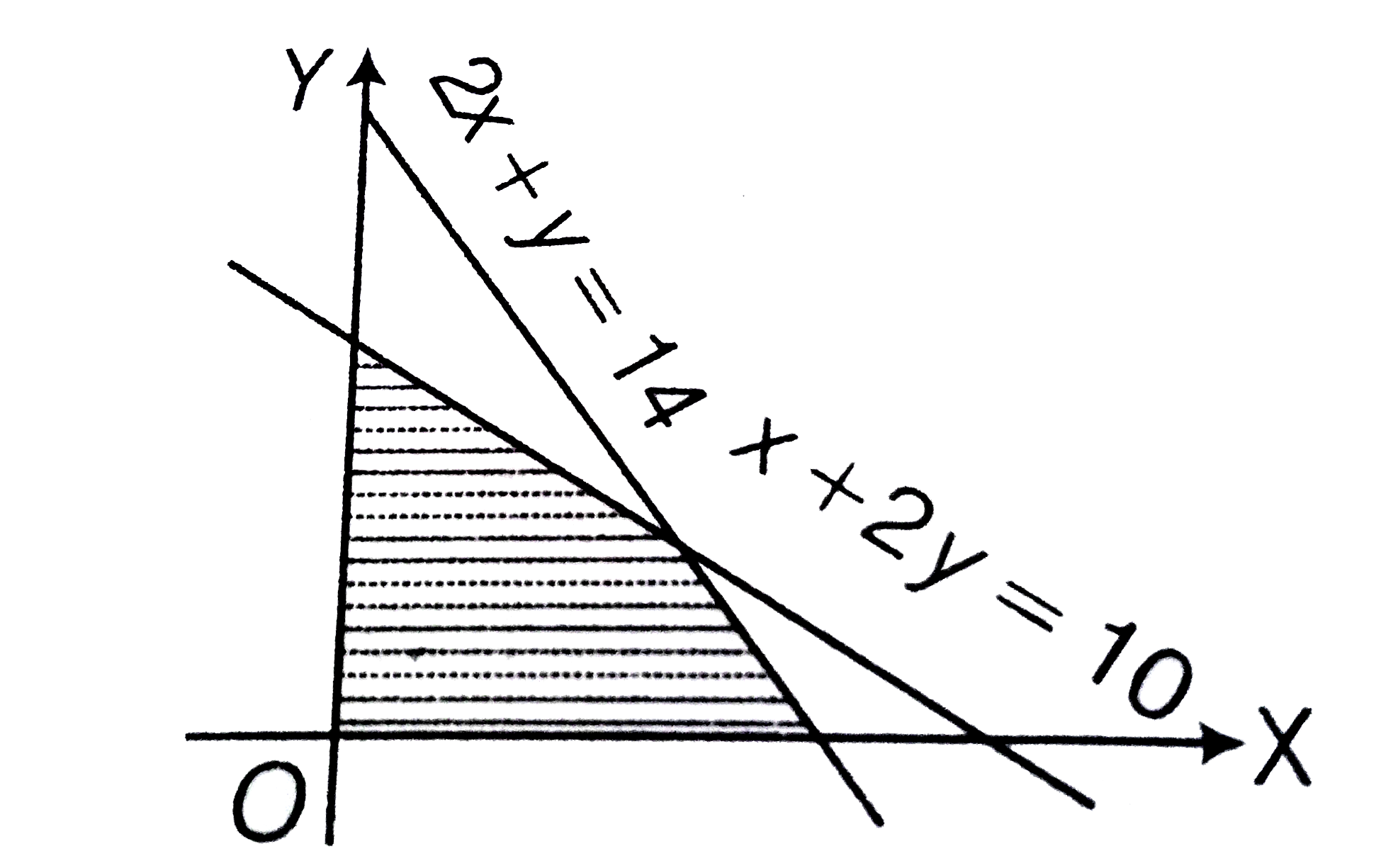
View Solution
Knowledge Check
Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IVAt the point of intersection of the two curves shown, the conc. of B is given by ……… for, A→nB:
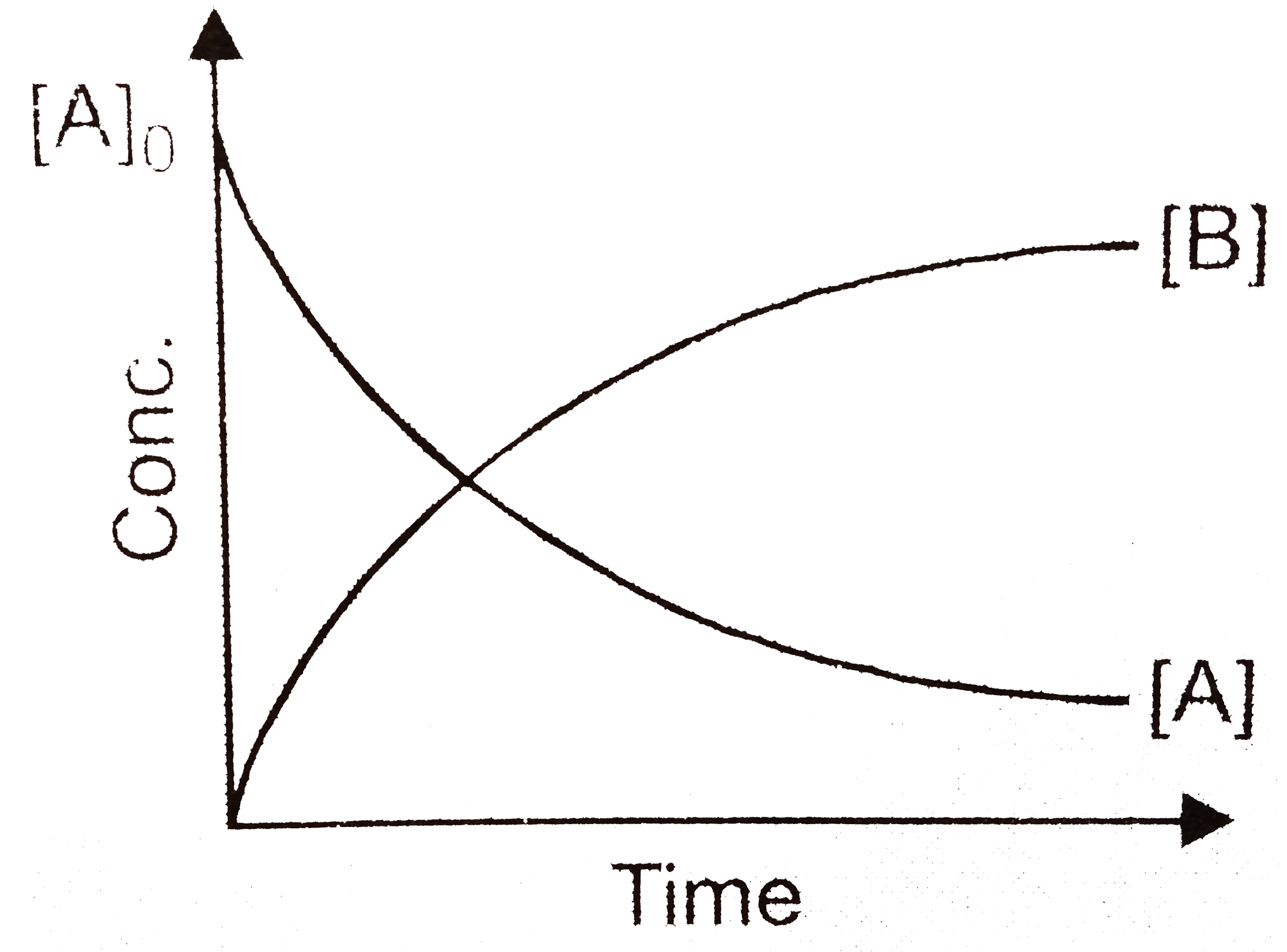 AnA02BA0n−1CnA0n+1D(n−1n+1)A0
AnA02BA0n−1CnA0n+1D(n−1n+1)A0The maximum or minimum of the objective funtion occurs only at the corner points of the feasible region. This theorem is known as fundamental theorem of
AAlgebraBArithmeticCCalculusDExtreme point
The maximum value of objective function Z=3x+y under given feasible region is
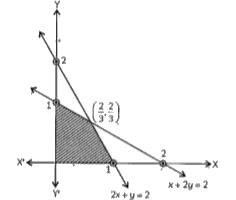
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionIn the given figure, name:

lines whose point of intersection is C
View SolutionAt the point of intersection of the two curves shown, the conc.of B is given by….. ….. ……….for, A→nB

View Solution
