The constraints −x1+x2≤1,−x1+3x2≤9,x1,x2>0 defines
A
bounded feasible space
B
unbounded feasible space
C
both bounded and unbounded feasible space
D
None of the above
Video Solution
Text Solution
The correct Answer is:B
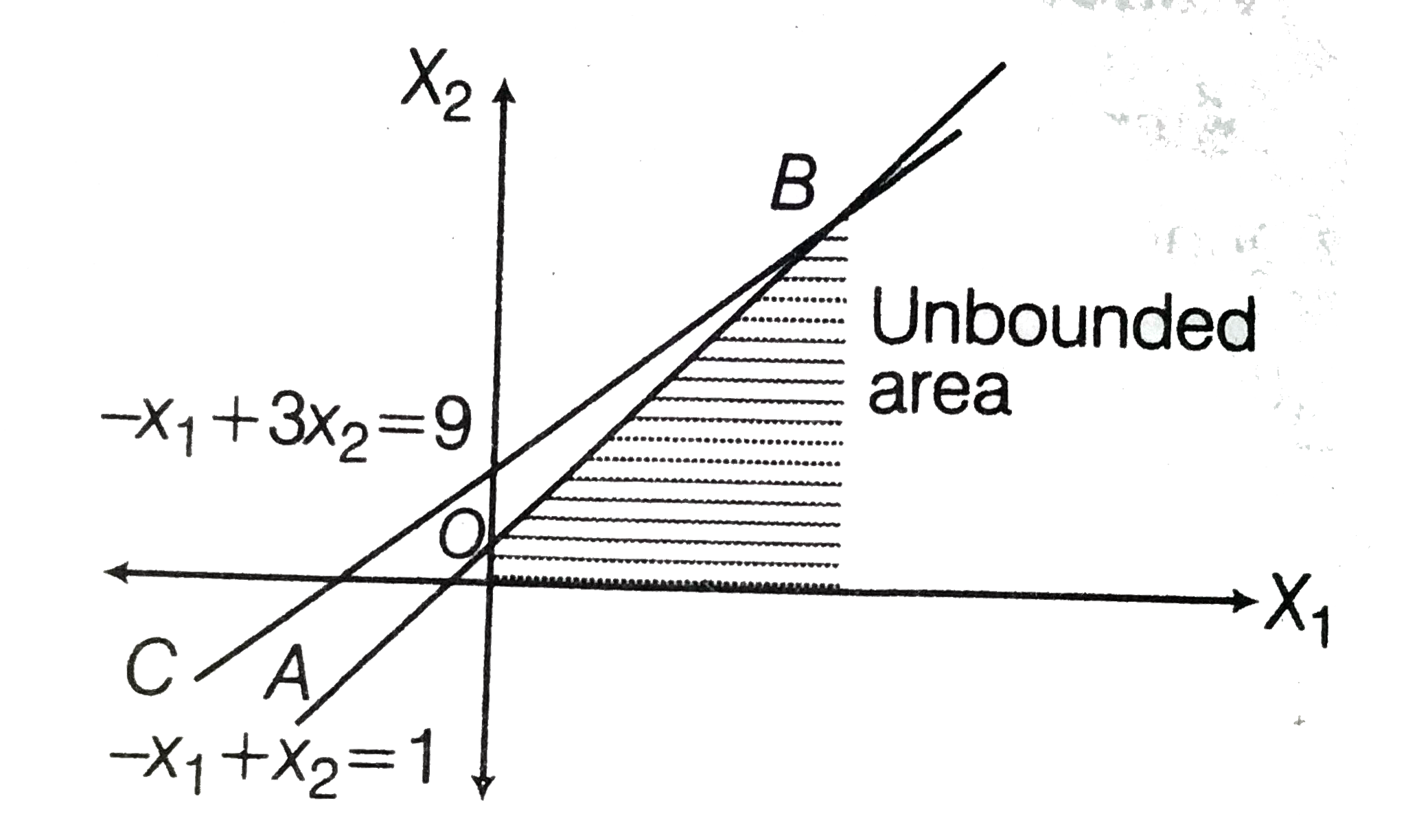
So, given constraints define unbounded feasible space.
|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
The constraints −x1+x2<1,−x1+3x2≤9,x1,x2>,0 difines on
Abounded feasible spaceBunbounded feasible spaceCboth bounded and unbounded feasible spaceDNone of the aboveBy graphical method, the solutions of linear programming problem maximum Z=3x1+5x2 subject to constraints 3x1+2x2≤18
x1≤4,x2≤6,x1≥0,x2≥0Ax1=2,x2=6,Z=36Bx1=2,x2=6,Z=36Cx1=4,x2=3,Z=27Dx1=4,x2=6,Z=42By graphical method, the solutions of linear programming problem maximise Z=3x1+5x2 subject to constraints 3x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 are
Ax1=2,x2=0,Z=6Bx1=2,x2=6,Z=36Cx1=4,x2=3,Z=27Dx1=4,x2=6,Z=42
The iinear programming problem Maximise Z=x1+x2
Subject to constraints
x1+2x2≤≤2000
x1+x2≤15000
x2≤600
x1≥has
View SolutionThe linear programming problem Maximise Z=x1+x2
Subject to constraints
x1+2x2≤2000x1+x2≤1500x2≤600x1≥0 has
View SolutionThe linear programming problem : Maximize z=z=x1+x2 subject to constraints x1+2x2≤2000,x1+x2≤1500,x2≤600,x1≥0 has
View SolutionThe objective function Z=x1+x2, subject to x1+x2≤10,−2x1+3x2≤15,xx1≤6,x1,x2≥0 has maximum value ________ of the feasible region .
View SolutionThe LPP problem Max z=x1+x2 such that −2x1+x2≤1,x1≤2,x1+x2≤3andx1,x2≥0 has
View Solution
