Area of the region bounded by the curves $y = 2^{x}, y = 2 x - x^{2}, x = 0 and x = 2$ is given by :

A

$3 / log 2 - 4 / 3 sq unit$

B

$3 / log 2 + 4 / 3 sq unit$

C

$3 log 2 + 4 / 3 sq unit$

D

$3 log 2 - 4 / 3 sq unit$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The two curves $y = 2^{x} \dots (i)$
and $y = 2 x - x^{2} \dots (i i)$
do not intersect between x = 0 and x = 2

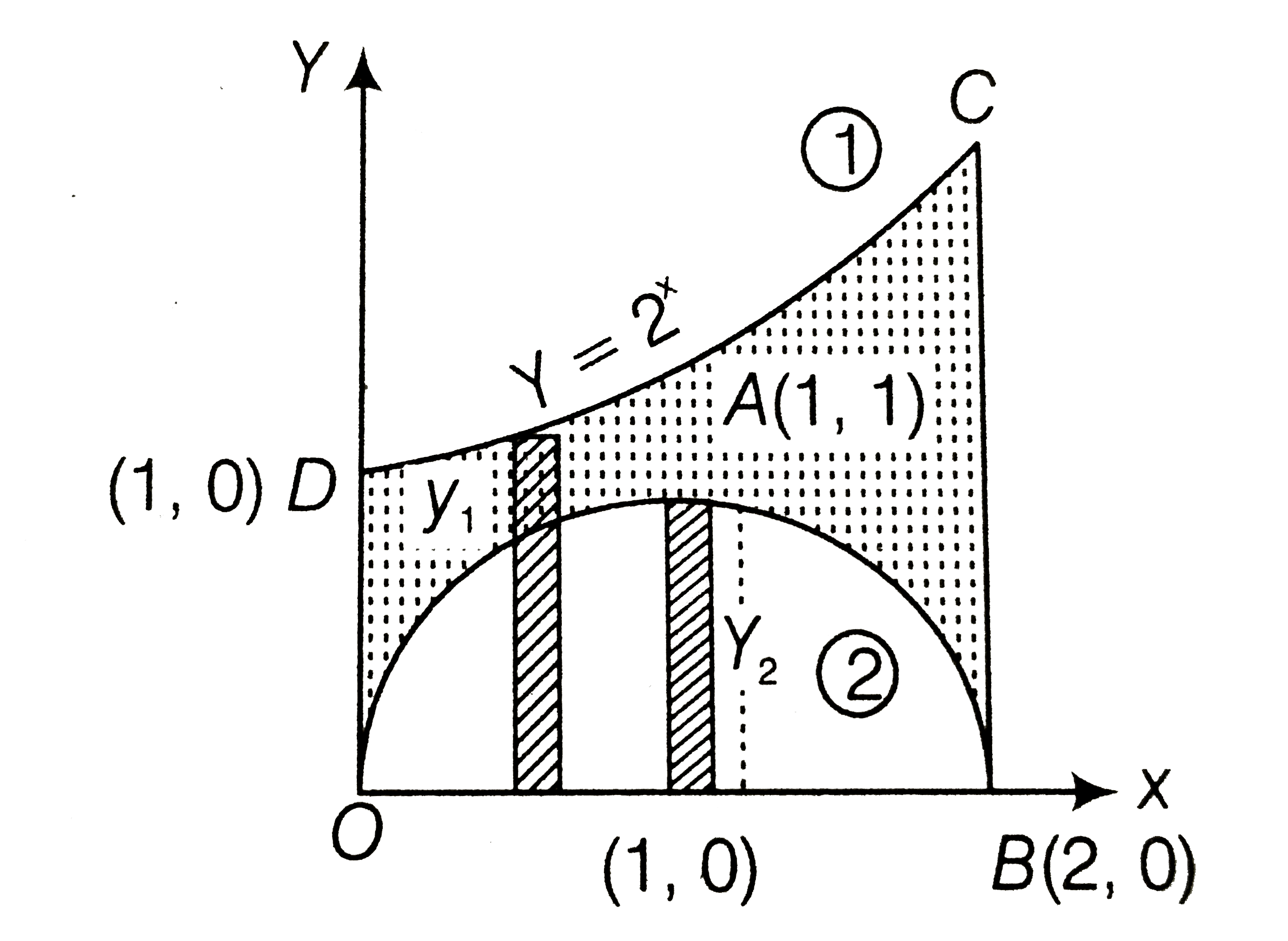
$∴$ Required area $= \int_{0}^{2} (2^{x} - 2 x - x^{2}) d x$
$= 3 / log 2 - 4 / 3 sq units$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by the curve $y = x sin x,$ x-axis, $x = 0$ and $x = 2 π$ is :
A $2 π$ sq. units
B $3 π$ sq. units
C $4 π$ sq. units
D $5 π$ sq. units
Question 2 - Select One
The area of the region bounded by the curve $y = 2 x - x^{2}$ and X- axis is
A $\frac{2}{3}$ sq.units
B $\frac{4}{3}$ sq.units
C $\frac{5}{3}$ sq.units
D $\frac{8}{3}$ sq.units

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 14-Paper 2 (Mathematics)

Home
Ask Doubt
Profile