For an LPP, minimise Z = 2x + y subject to constraint 5x+10y≤50,x+y≥1,y≤4 and x,y≥0 then Z is equal to
A
0
B
1
C
2
D
12
Video Solution
Text Solution
The correct Answer is:B
The vertices of a feasible region are A(0,1),B(1,0),C(10,0),D(2,4),E(0,4).
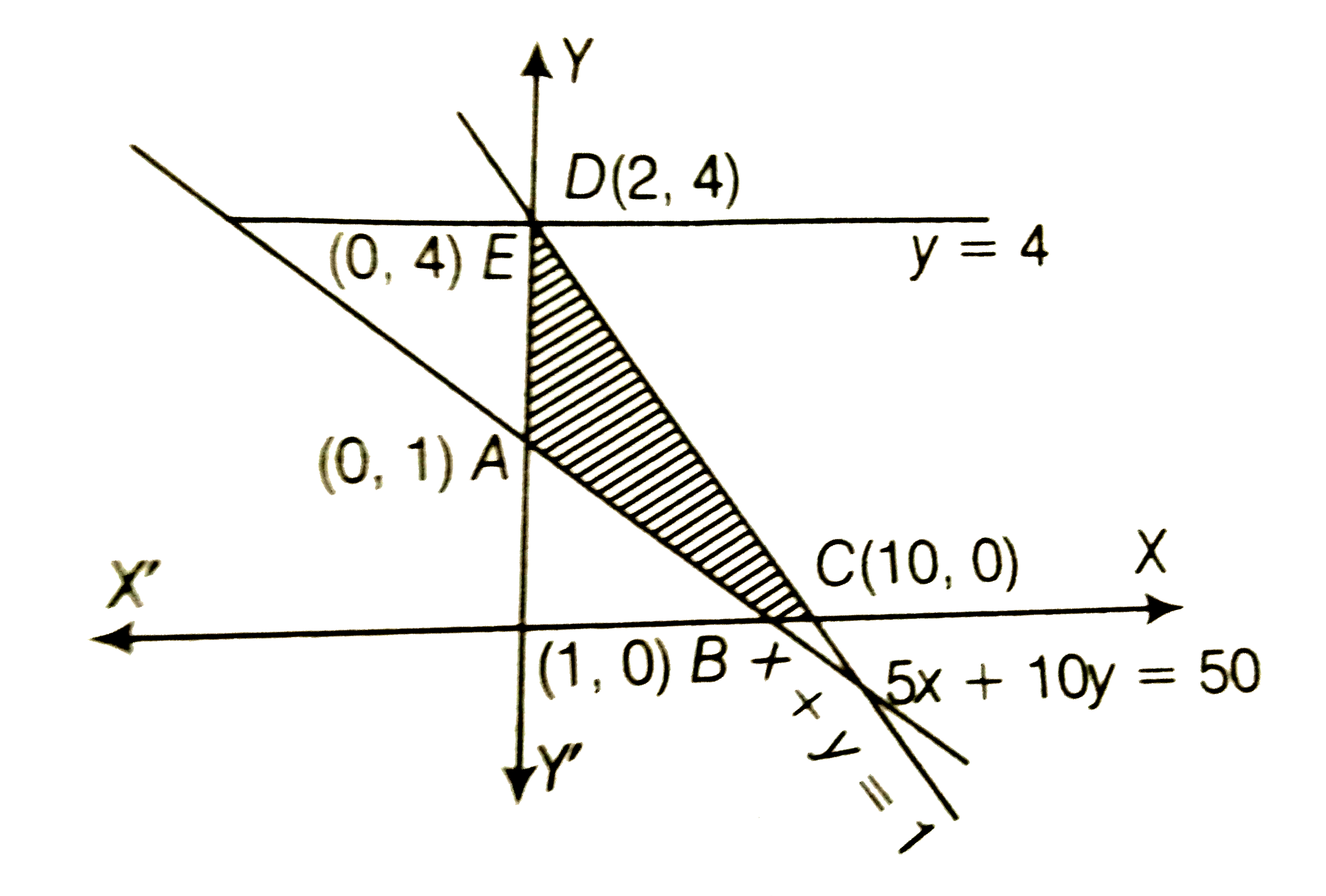
Given, z=2x+y
At A(0,1),z=2(0)+1=1
At B(1,0),z=2(1)+0=2
At C(10,0),z=2×10+0=20
At D(2,4),z=2×2+4=8
and at E(0,4),z=2×0+4=4
Hence, minimum value is 1.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Maximum value of Z = 12x + 3y subject to constraints x≥0,y≥0,x+y≤5 and 3x+y≤9 is
A15B36C60D40
Maximize z=2x+3y subject to constraints x+4y≤8,3x+2y≤14,x≥0,y≥0.
View SolutionMinimize Z=−3x+4y subject ot constraints : x+2y≤8,3x+2y≤12,x≥0,y≥0.
View SolutionMaximize Z=400x+500y subject to constraints x+2y≤80,2x+y≤90,x≥0,y≥0
View SolutionMinimize Z=3x+2y subject to the constraints : x+y≥8,3x+5y≤15,x≥0,y≥0.
View SolutionMaximize Z=5x+3y subject to the constraints: 3x+5y≤15,5x+2y≤10,x≥0,y≥0
View SolutionMaximize :
Z=x+y,subject to the constraints:
x−y≤−1,−x+y≤0,x≥0,y≥0
View SolutionMaximise Z=3x+4y, Subjected to the constraints x+y≤1,x≥0,y≥0
View Solution
