The number of critical points of
f(x)=|x|(x−1)(x−2)(x−3) is
A
1
B
2
C
3
D
4
Video Solution
Text Solution
The correct Answer is:D
Given,
f(x)=|x|(x−1)(x−2)(x−3)
=x(x−1)(x−2)(x−3),x≥0
−x(x−1)(x−2)(x−3),x<0
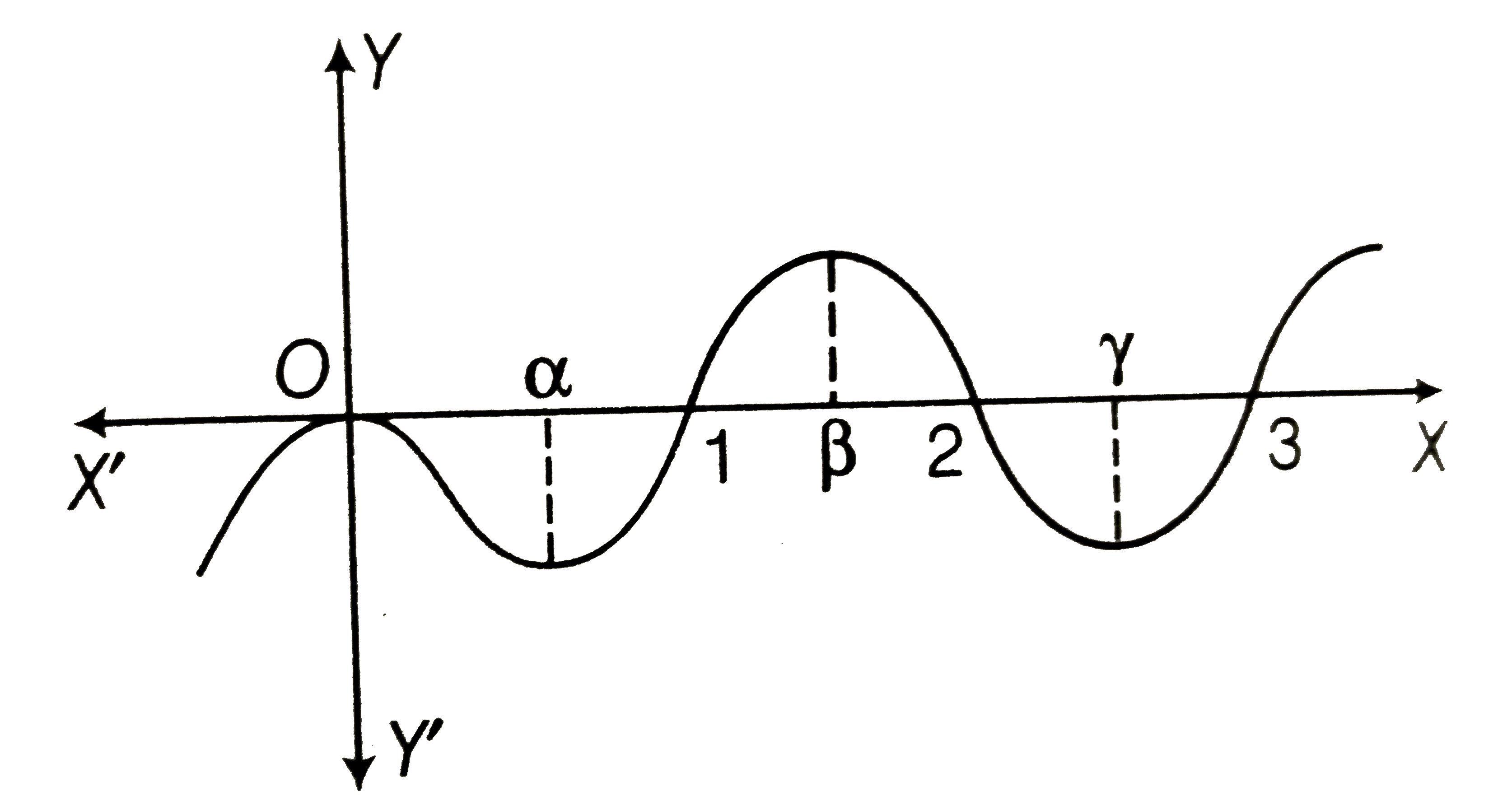
It is clear from the figure that, there are four critical points ie, 0,α,β,λ.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of critical points of f(x)=|x−1|−1x2is
A1B2C3Dnone of theseThe number of critical points of f(x)=(∫x0(cos2t−3√t)dt)+34x4/3−x+12 in (0,6π] is:
A10B8C6D12
The number of critical points of the function f(x)=|x−1||x−2| is
View SolutionThe critical points of f(x)=|2−x|x2 are
View SolutionThe number of points of maxima/minima of f(x)=x(x+1)(x+2)(x+3) is
View SolutionThe number of critical points of the functionf(x)=∫x0et(t−1)(t−2)(t−3)dt
View SolutionFind the critical points of f(x)=x2/3(2x−1)
View SolutionFind the number of critical points of the function
f(x)=|x−2|+|x+1|,x∈R
View Solution

