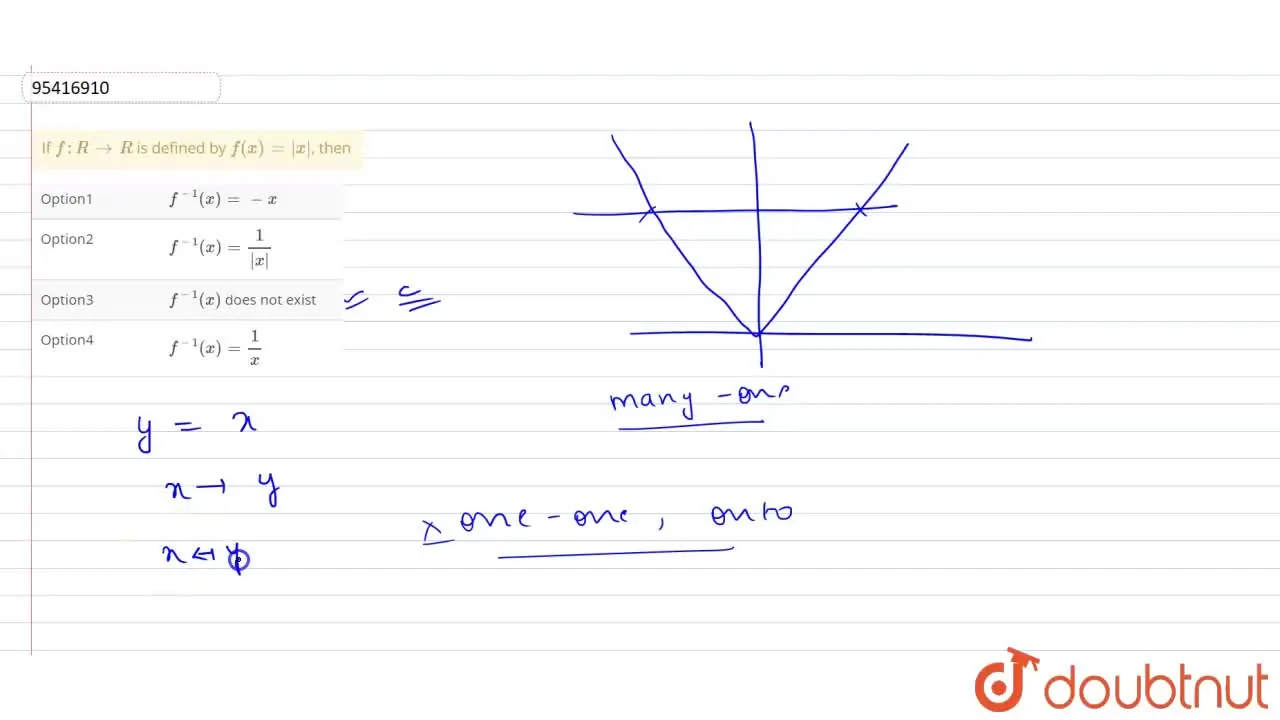
If is defined by , then
does not exist
The correct Answer is:C
Since is a many-one function so its inverse does not exist.
Related Playlists
Similar Questions
If f:R→R is defined byf(x)=|x|, then
View SolutionLet the f:R→R be defined by f(x)=2x+cosx. Then f:
View SolutionConsider the real function f:R→R, defined by
f(x)=⎧⎪⎨⎪⎩1−x,when x<01,when x=0x+1,when x>0
Write its domain and range. Also, draw the graph of f(x).View SolutionStudents of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y=x−4 . Let L be the set of all lines which are parallel on the ground and R be a relation on L.

Answer the following using the above information.
Let f:R→R be defined by f(x)=x−4. Then the range of o f(x) is _View SolutionIf f:R→R is defined by f(x)=3x+2, define f [f(x)].
View SolutionLet f:R→R be defined by f(x)=x1+x2,x∈R. Then the range of f is
View Solutionif f:R→R is defined as f(x)=e|x|−e−x then the correct statements(s) is/are
View SolutionDraw the graph of the signum function, f:R→R, defined by
f(x)=⎧⎪⎨⎪⎩x|x|,when x≠00,when x=0orf(x)=⎧⎪⎨⎪⎩1,if x>00,if x=0−1,if x<0View SolutionIf : R→ R defined by f(x)=x|x|, then f(x) is
View SolutionIf f:R→R is defined by f(x)=x2−3x+2, write f{f(x)}.
View Solution