A circle with centre at (2, 4) is such that the line x+y+2=0 cuts a chord of length 6. The radius of the circle is
A
√41 cm
B
√11 cm
C
√21cm
D
√31cm
Video Solution
Text Solution
The correct Answer is:A
Let r be the radius of the circle.
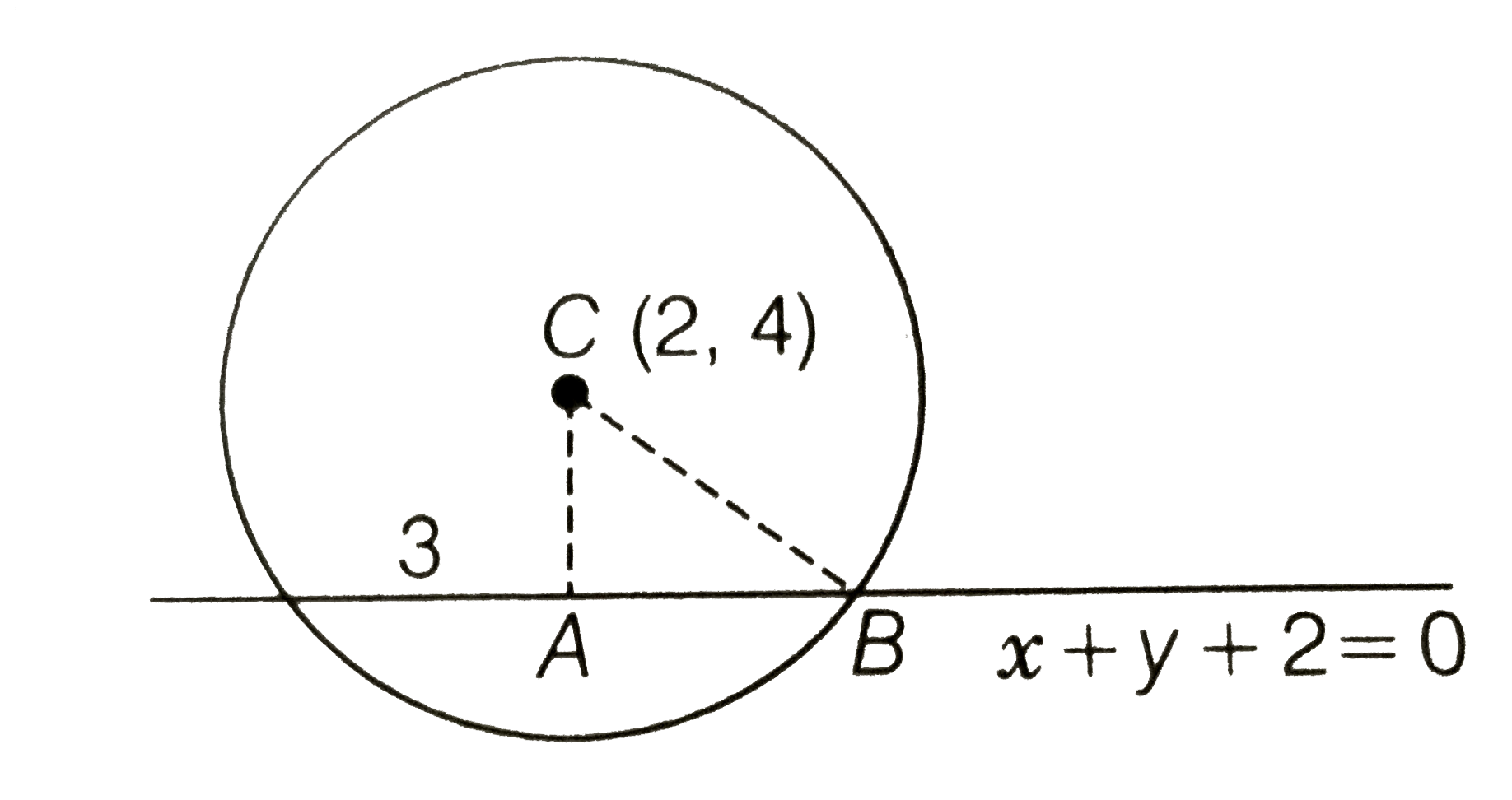
Now perpendicular distance
AC=|2+4+2|√12+12
=8√2=4√2
In right angled ΔCAB,
r2=(AC)2+(AB)2
=(4√2)2+(3)2=32+9
⇒r2=41
∴r=√41
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The square of the radius of the circle is
A45B75C20D50If the line x+2y=3 cuts a chord of length r unit with the circle x2+y2=r2 then find r2.
A125B√12C512D√125In a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cm
The line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4. The radius of the circle is
View SolutionA circle x2+y2=1 cuts the line x+y=k and makes chord with length 1. The value of |K| is:
View SolutionThe line 2x−y+1=0is tangent to the circle at the point (2,5) and the centre of the circles lies on x−2y=4 The radius of the circle is:
View SolutionA diameter of x2+y2−2x−6y+6=0 is a chord to circle centre (2, 1), then radius of the circle is
View Solution