Draw the graph of the signum function, f:R→R, defined by
f(x)=⎧⎪⎨⎪⎩x|x|,when x≠00,when x=0orf(x)=⎧⎪⎨⎪⎩1,if x>00,if x=0−1,if x<0
Video Solution
Text Solution
Clearly, we have
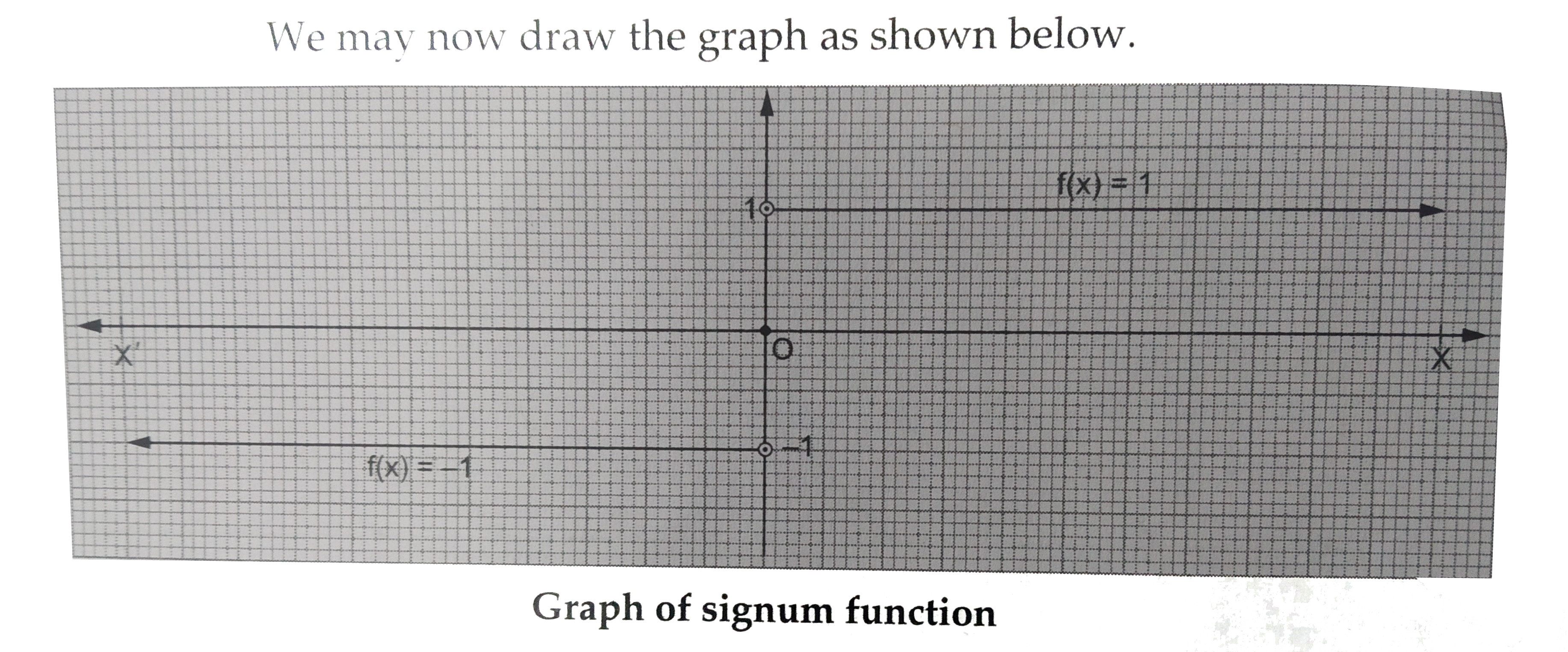
x<0⇒f(x)=−1
x=0⇒f(x)=0
x>=0⇒f(x)=1.
We may now draw the graph as shown below.
|
Topper's Solved these Questions
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - PROBLEMS BASED ON DOMANIS AND RANGES OF REAL FUNCTIONS SOLVED EXAMPLES
23 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - SOLVED EXAMPLES
20 Videos
- ELLIPSEBOOK - RS AGGARWALCHAPTER - ELLIPSEEXERCISE - EXERCISE
26 Videos
- GEOMETRICAL PROGRESSIONBOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12H (Very Short Answer Type Questions)
13 Videos
Similar Questions
Knowledge Check
f(x)={x2x2+|x|x≠01x=0then f(x) is
Acontinuous but non- differentiable at x=0Bdifferentiable at x=0Cdiscontinuous at x=0Dnone of theseIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x−1,x<014,x=0x2,x>0 , then
Alimx→0+f(x)=1Blimx→0−f(x)=1Cf (X) is discontinuous at x = 0DNone of these
Draw the graph of the signum function f(x)={|x|x when x≠00 when x=0
View SolutionExamine the continuity of the function f(x) at x = 0.
f(x)=⎧⎨⎩tan2x3xwhen x≠032 when x=0
View SolutionShow that the following functions are continuous at x = 0 :
f(x)={xcos1x when x≠00 when x=0
View SolutionExamine the continuity of the function f(x) at x = 0.
f(x)={sinxx when x≠02 when x=0
View SolutionExamine the function for continuity at x = 0 :
f(x)={sinxx when x<0x+1 when x≥0.
View SolutionLet f(x)={|x|x,x≠00,x=0.
Find limx→0f(x).
View Solution
