To maximise the objective function z = x + 2 y under the constraints x - y ≤ 2 , x + y ≤ 4 and x , y ≥ 0 is

A

1x=0,y=4,z=8

B

x = 1 , y = 2 , z = 5

C

x = 1 , y = 4 , z = 9

D

x = 0 , y = 3 , z = 6

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

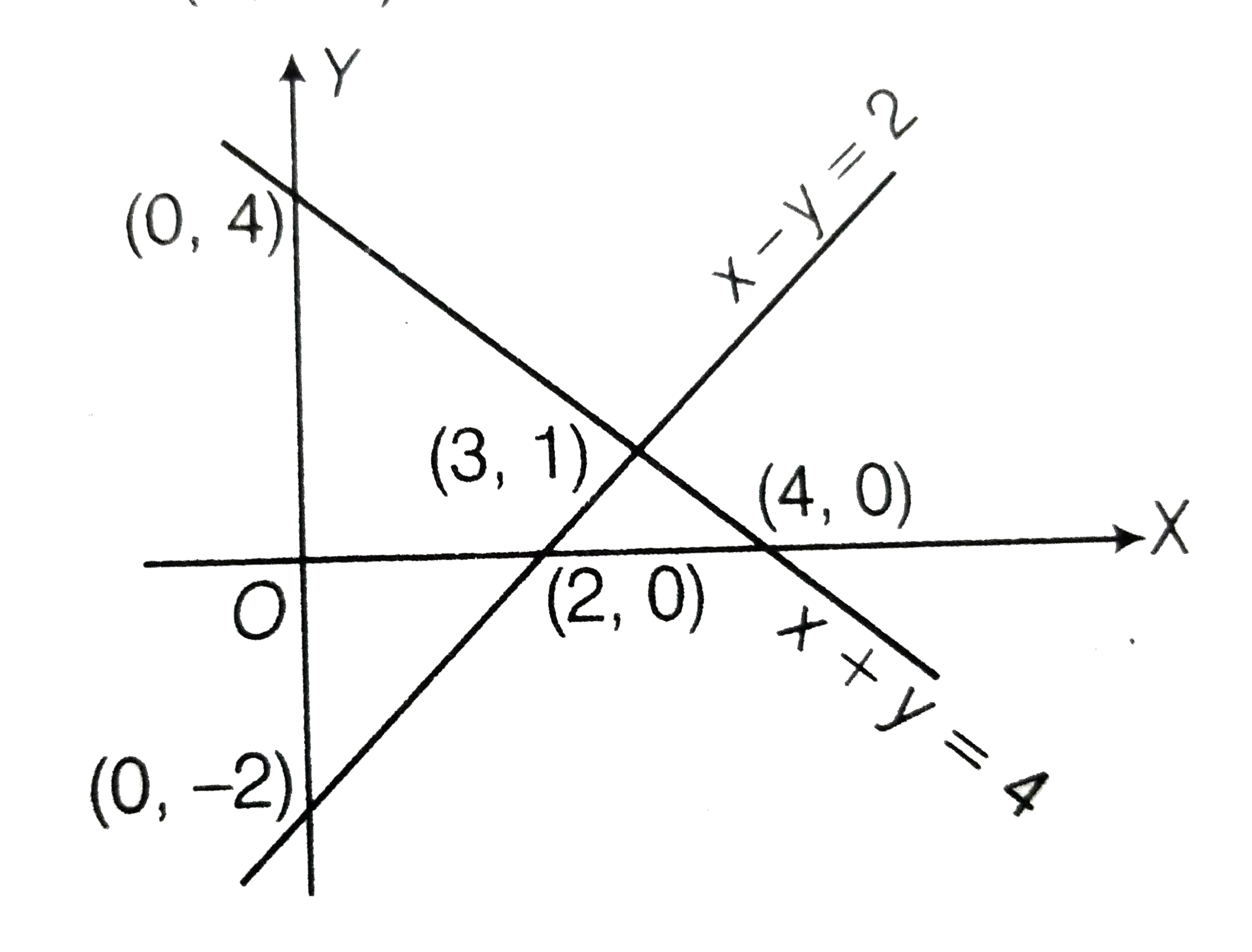
Given, x - y = 2 ⇒ x 2 + y - 2 = 1
This line meets the exes at (2,0) ltbRgt and (0,-2).
ocr_image
No x+y=14
⇒ x 4 + y 4 = 1
This line meets the axes at (4,0)
and (0,4). Now, at point (0,4), z=0+4 × 2=8
at point ( 2 , 0 ) , z = 2 + 0 = 2
and at point ( 3 , 1 ) , z = 3 + 2 = 5
Thus, function is maximum at (0,4) and maximum value is 8.

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The minimum value of linear objective function z=2x+2y under linear constraints 3x+2y≥12,x+3y≥11andx,y≥0 is

    A10
    B12
    C6
    D5

  • The minimum value of linear objective function z =2x + 2y under linear constraints 3x+2y≥12,x+3y≥11andx,y≥0 is

    A10
    B12
    C6
    D5

  • The maximum value of the objective function Z=3x+2y for linear constraints x+y≤7,2x+3y≤16,x≥0,y≥0 is

    A16
    B21
    C25
    D28