The constraints −x+y≤1,−x+3y≤9,x≥0,y≥0 defines
A
bounded feasible region
B
unbounded feasible region
C
both bounded and unbounded region
D
unique solution
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for The constraints -x+yle1,-x+3yle9,xge0,yge0 defines by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Shaded, region of the constraints 4x+3y≤12,−x+y≤2,x≥0,y≥0 is
A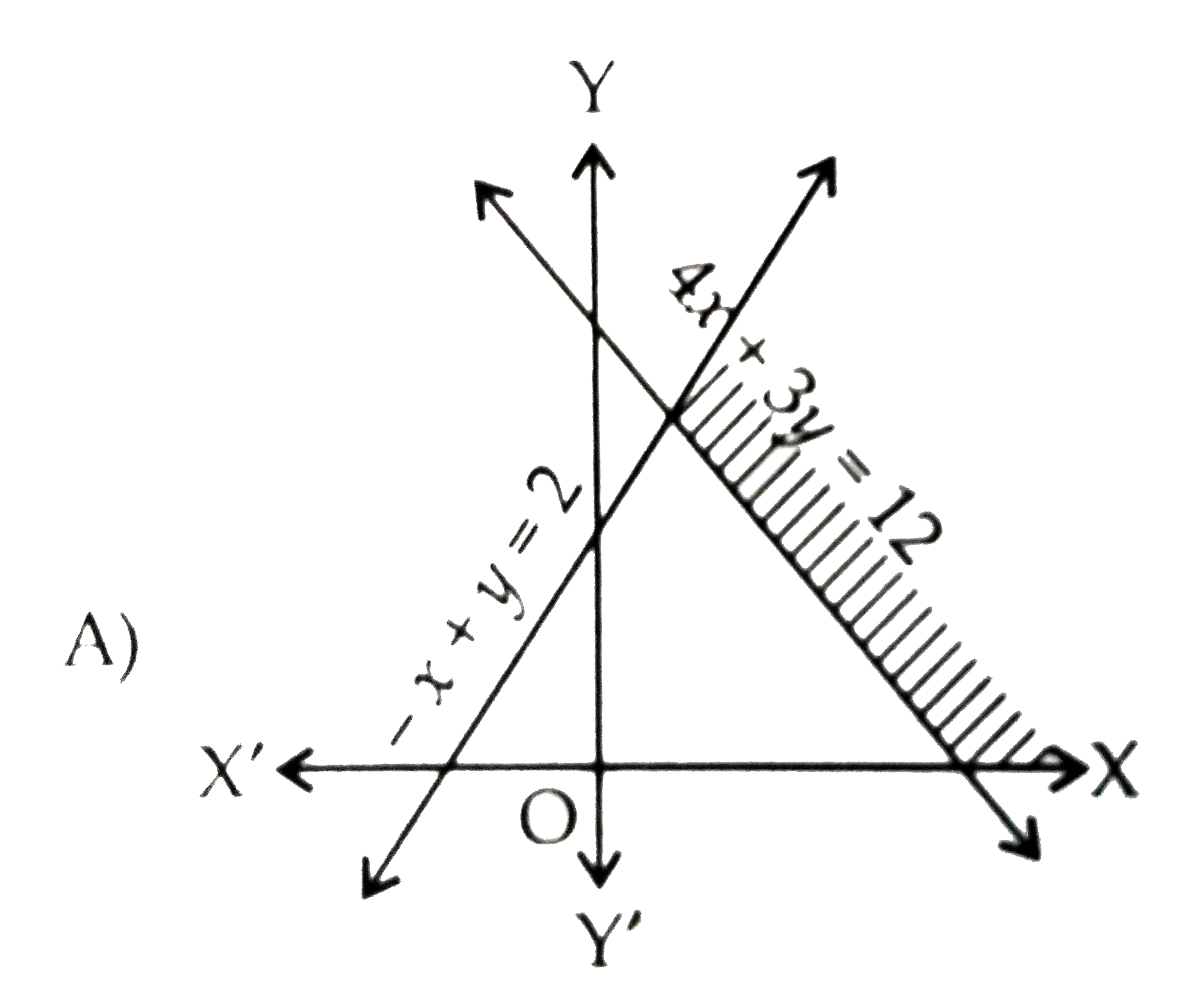 B
B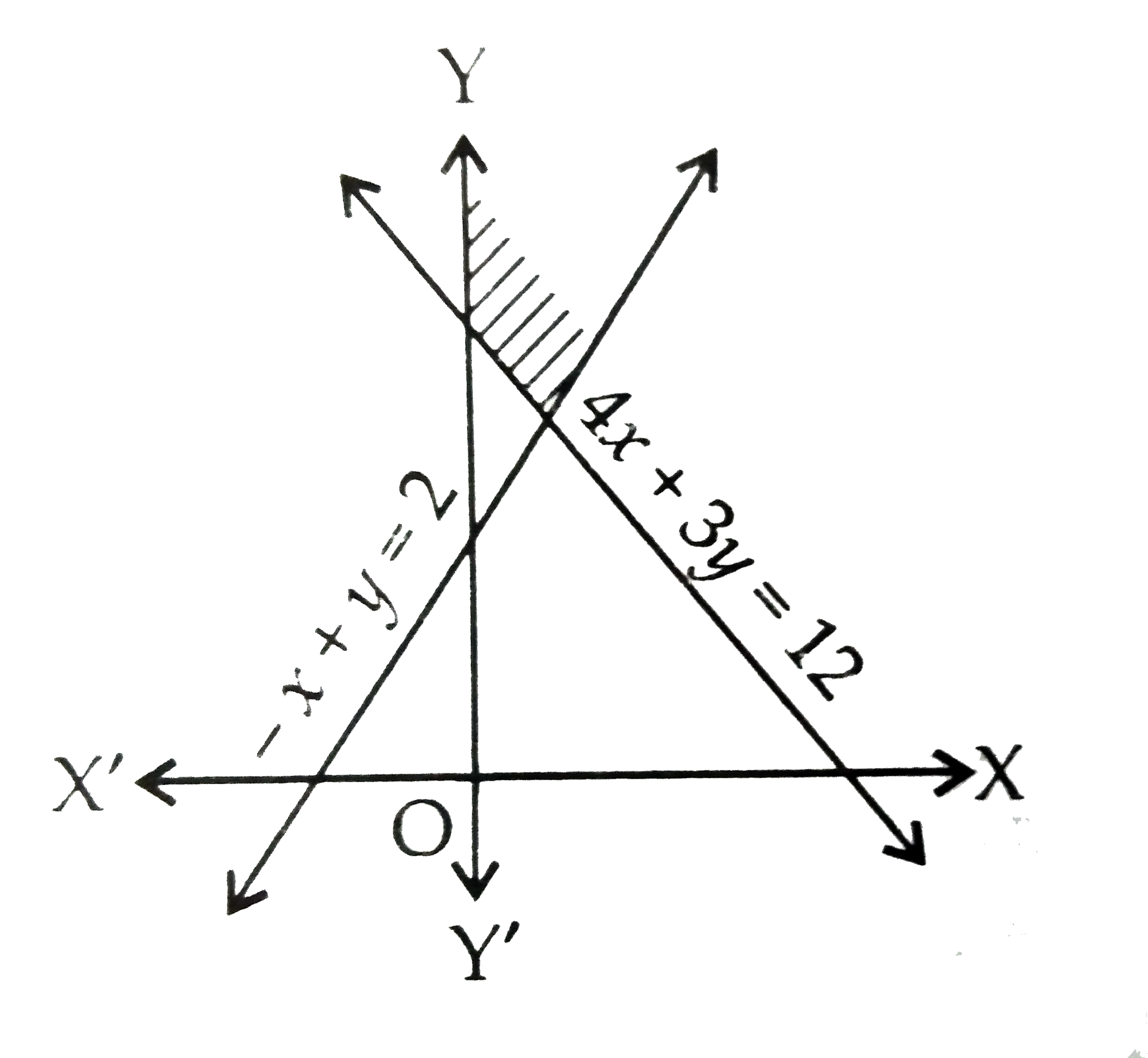 C
C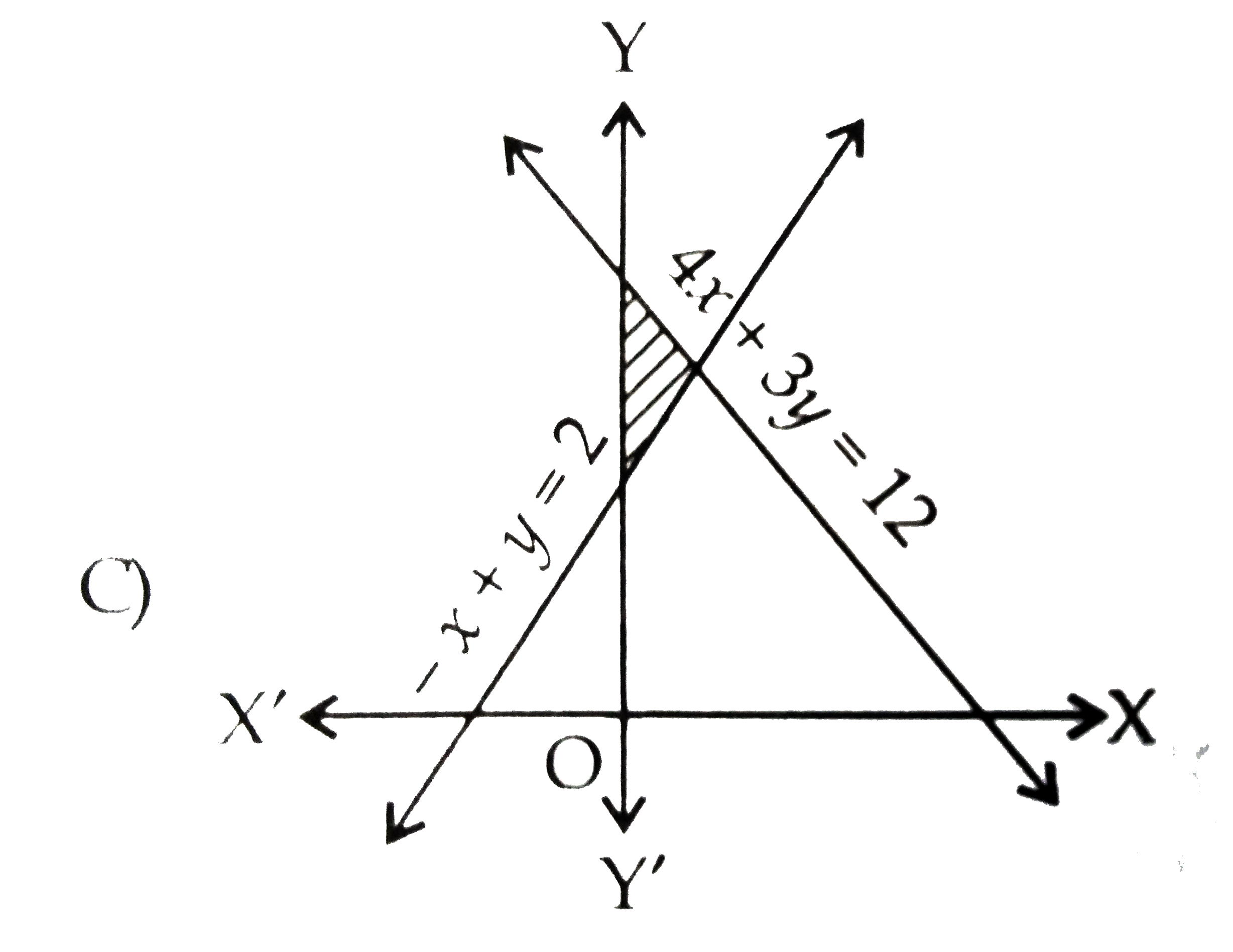 D
D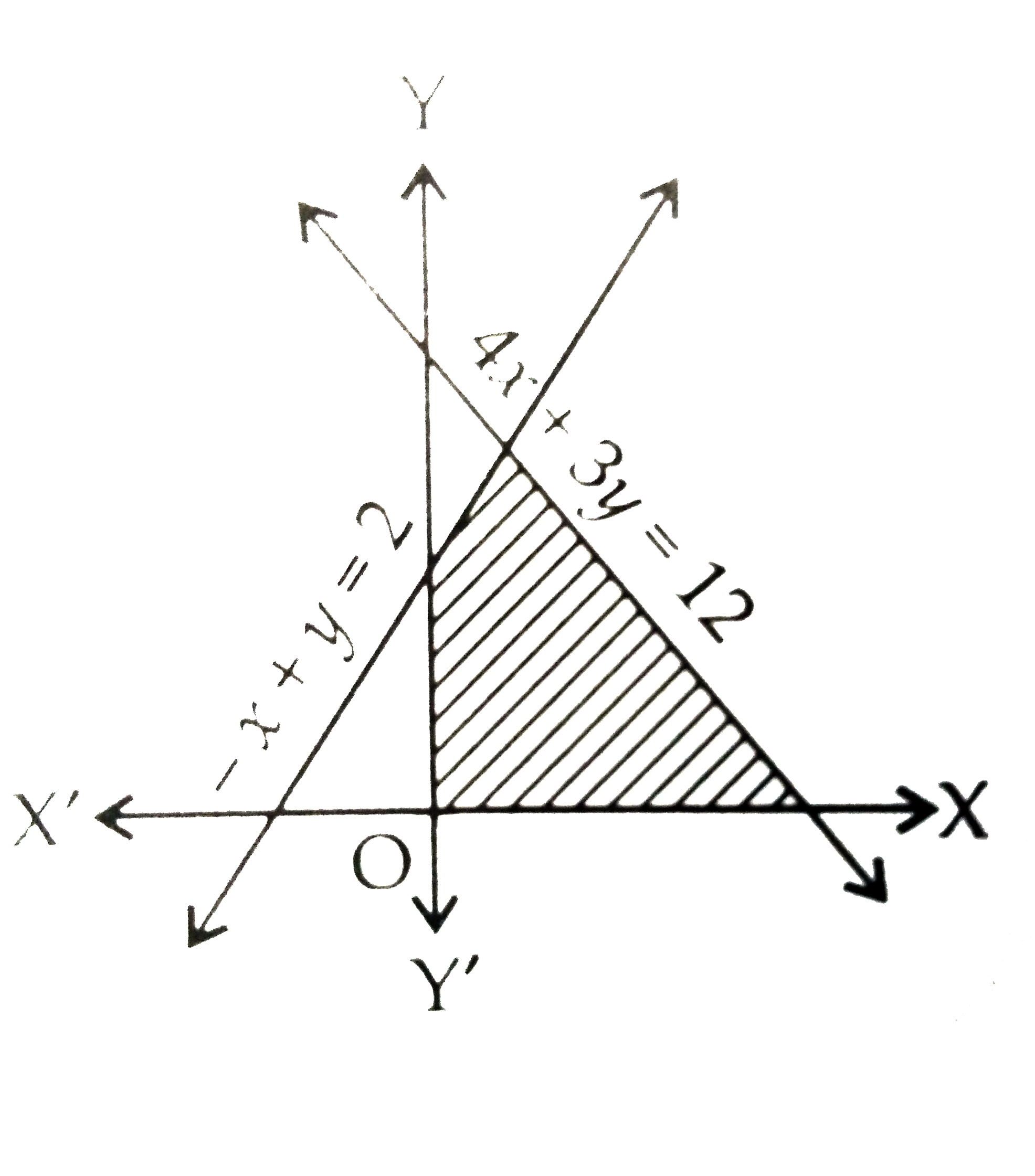
The contraints −x+y≤1,−x+3y≤9,x≥0,y≥0 of LLP correspond to
Abounded feasible regionBunbounded feasible regionCboth bounded and unbounded feasible regionDneither bounded nor unbounded regionThe constraints x−y≥0,−x+3y≤3,x≥0,y≥0 and the objective function z=6x+8y has
Aunbounded solutionBconcave solutionCbounded solutionDunique solution
The maximum vlaue of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0 is
View SolutionThe maximum of z = 5x+2y , subject to the constrainsts x+y≤7,x+2y≤10,x,y≥0 is
View SolutionThe maximum value of z = 4x +2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
View SolutionShaded, region of the constraints x+y≥5,2x+3y≤18,4x+3y≤24,x≥0,y≥0 is
View SolutionThe maximum value of P = 3x +4y subject to the constraints x+y≤40,2y≤60,x≥0andy≥0 is
View Solution
