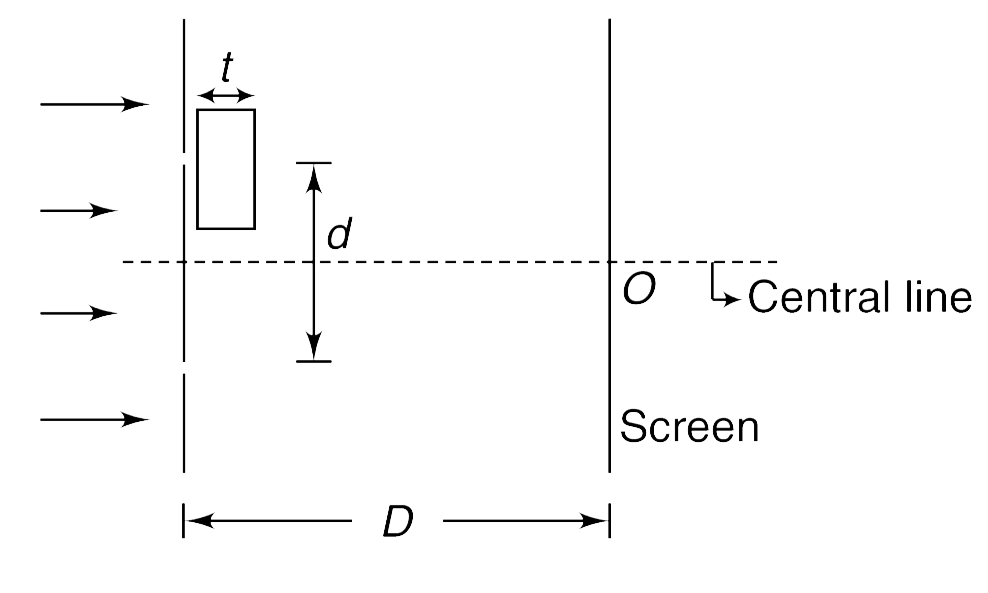
In YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
β(μ−1)t2λ
β(μ−1)tλ
β(μ−1)t3λ
β(μ−1)t4λ
The correct Answer is:B
Step by step video, text & image solution for In YDSE, slab of thickness t and refractive index mu is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength lamda is incident on system is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a YDSE experiment, the distance between the slits & the screen is 100cm. For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25mm. When the distance between the slits is increased by Δd=1.2mm, the fringe width decreased to n=2/3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light.
View SolutionIn Young’s double slit experiment a transparent sheet of thickness t and refractive index μ is placed in front of one of the slits and the central fringe moves away from the central line. It was found that when temperature was raised byΔθthe central fringe was back on the central line (at C). It is known that temperature coefficient of linear expan- sion of the material of the transparent sheet isα. A young scientist modeled that the refractive index of the material changes with temperature as Δμ=–gamaΔθ. Find Δθ in terms of other given quantities. D and d are given and have usual meaning.
View Solution
Knowledge Check
In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)In the Young's double slit experiment , a mica slip of thickness t and refractive index μ is introduced in the ray from first source S1 . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
AdD(μ−1)tBDd(μ−1)tCd(μ−1)DDDt(μ−1)In YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
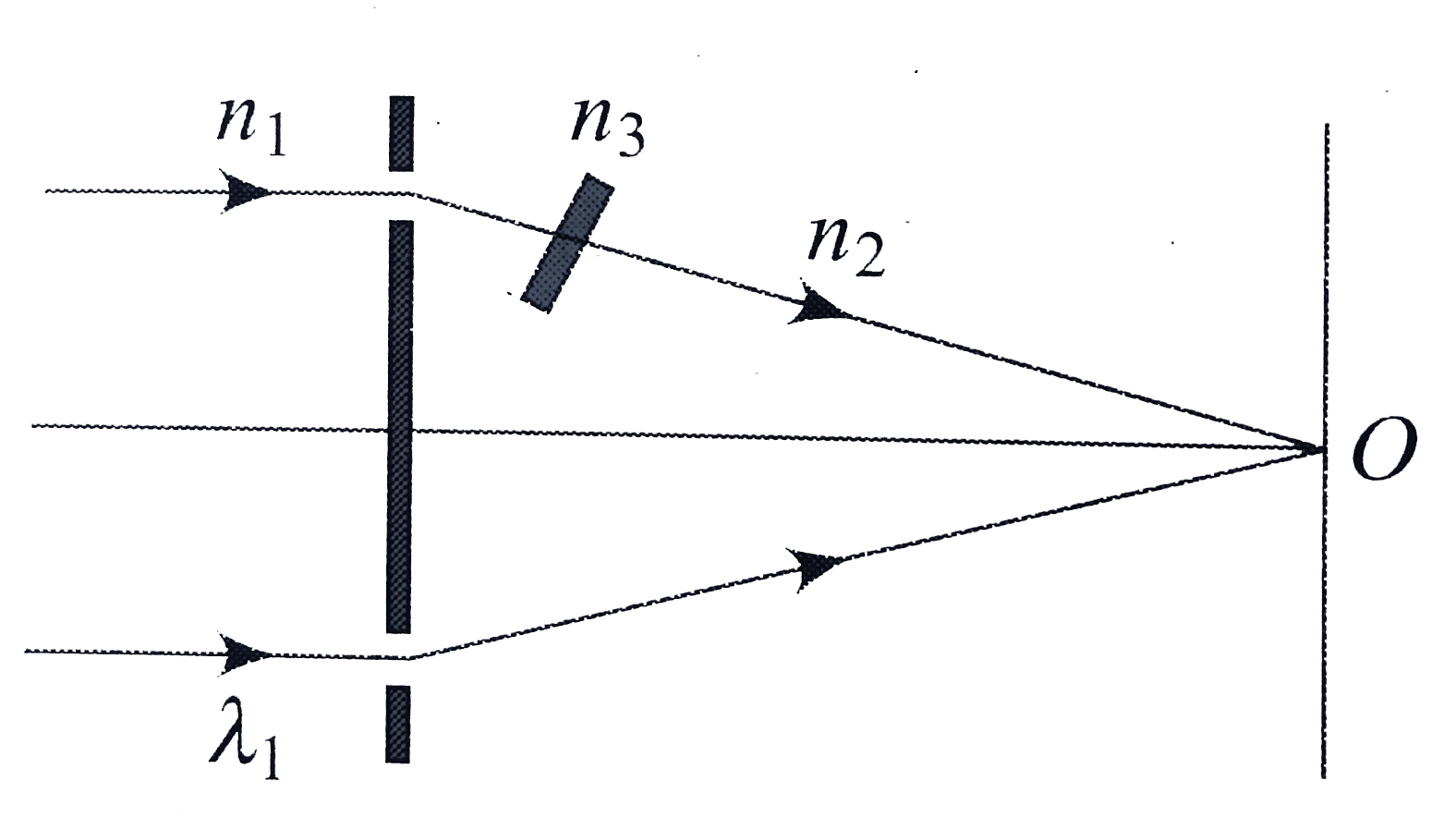 A2πn1λ1(n3−n2)tB2πλ1(n3−n2)tC2πn1n2λ1(n3n2−1)tD2πn1λ1(n3−n2)t
A2πn1λ1(n3−n2)tB2πλ1(n3−n2)tC2πn1n2λ1(n3n2−1)tD2πn1λ1(n3−n2)t
A plate of thickness t made of material of refractive index μ is placed in front of one of the slits in a double slit experiment . What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ?
View SolutionA plate of thickness t made of a material of refractive index μ is placed in front of one of the slits in a double slit experiment. (a) Find the changes in he optical path due to introduction of the plate. (b) Wht should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ? Wavelength of the light used is λ. Neglect any absorption of light in the plate.
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
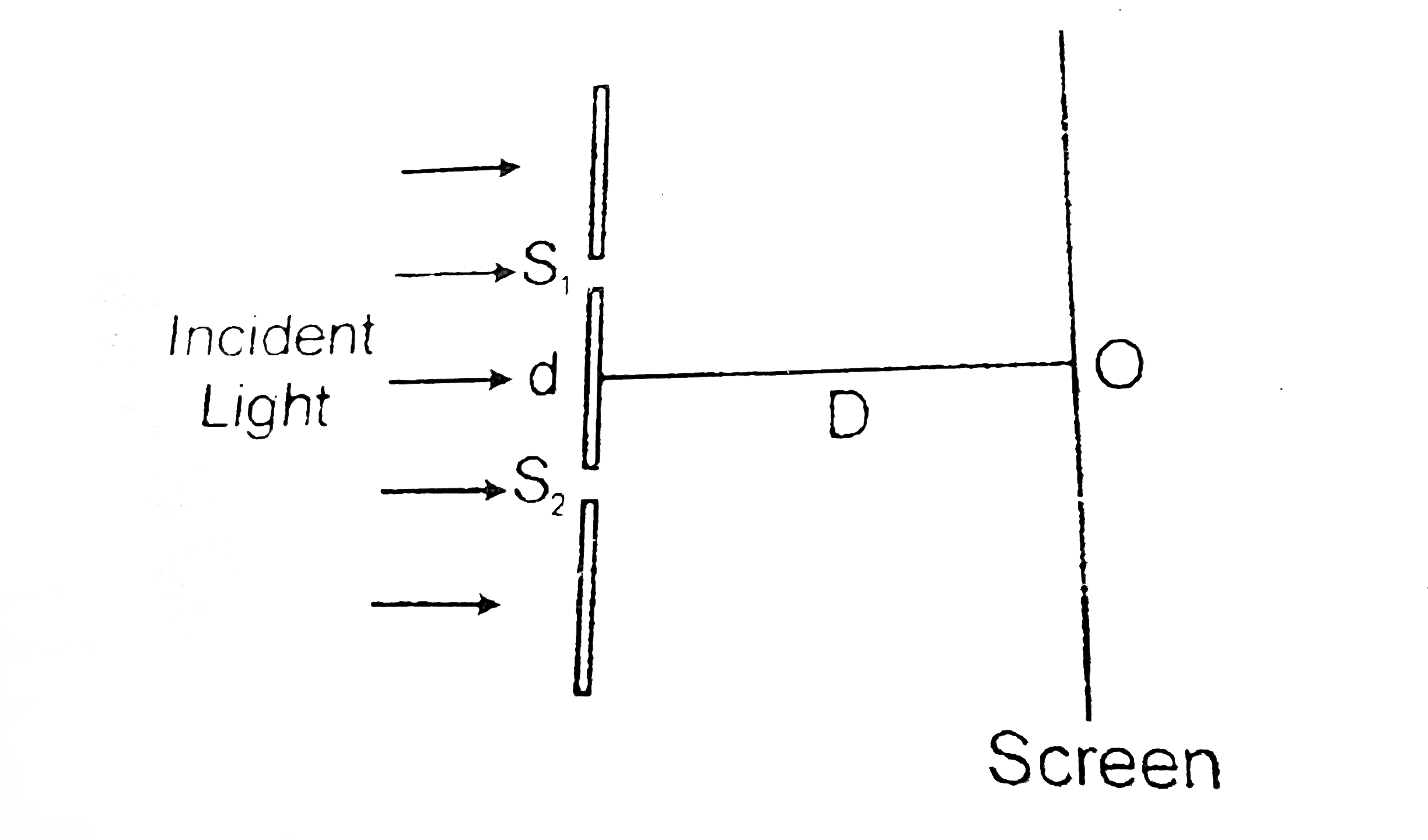
After placing the film of slit S1, the intensity at point O screen is :
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionIn a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
View Solution
