A rectangular conducting loop, PQRS is hanging from a thread as shown. Thread is now cut. Compute velocity with which the loop falls as function of time t. Show that if side PS is large enough the loop ultimately falls with constant speed. (m = mass of loop, r = Resistance of loop, PQ = l, PS = b)

Strategy : At any time t, let current in loop (direction of which is given by Lnez's law) and velocity of the loop are i and v respectively. Forces acting on the loop are mg (downwards) and magnetic force Bil (upward).
(i) By Newton's second law,
F = ma
⇒mg−Bil=mdvdt
⇒mg−B(Bvlr)l=mdvdt
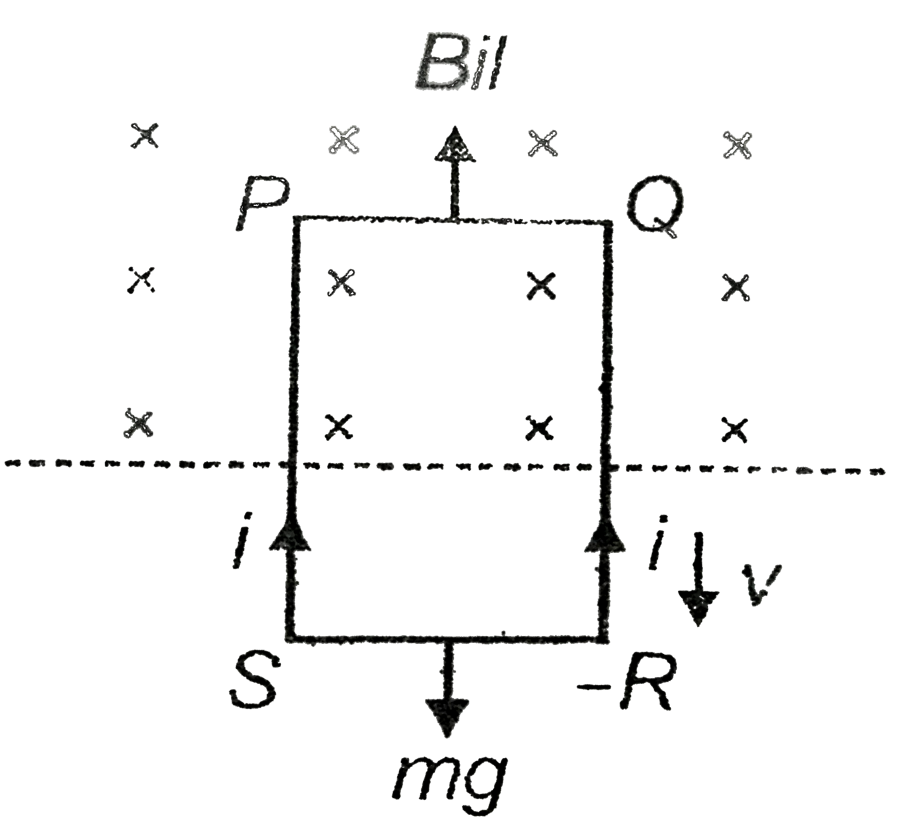
⇒dtm=dvmg−B2vl2r
⇒∫t0dtm=∫v0dvmg−B2vl2r
⇒tm⎡⎢
⎢⎣ln[mg−B2vl2r]−B2l2r⎫⎪
⎪⎬⎪
⎪⎭v0
⇒−B2l2mrt=ln⎡⎢⎣mg−B2vl2rmg⎤⎥⎦
⇒v=rmgB20l2[1−e−B2l2tmr]
(ii) Velocity variation can be shown graphically, as in the graph here,
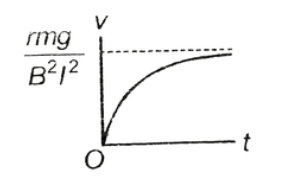
Therefore after long-time it can be seen the loop will fall with constant speed (called terminal speed) equal to rmgB2l2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
41 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
46 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION -J(Aakash Challengers Questions)
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
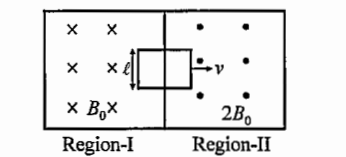
A conducting loop is being pulled with speed v from region I of magnetic field to region II. If resistance of the loop is R, current induced in the loop at the instant shown is
View SolutionA conducting square loop of side 10 cm is placed in a region of uniform magnetic field 0.5 T as shown in the figure. Calculate the work done in slowly moving the loop out of the field in 2 seconds with a speed of 0.05ms−1. The resistance of loop is 10 Ω.

View Solution
Knowledge Check
a conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzeroA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzeroA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
 A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
Space is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
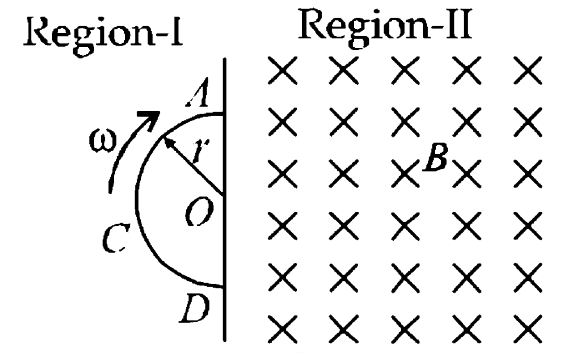
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
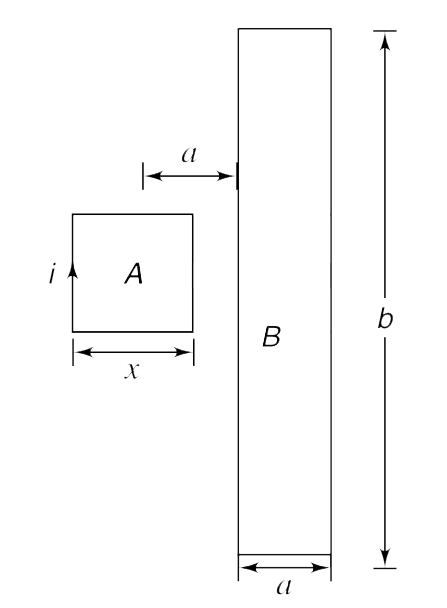
View SolutionA rectangular conducting loop B has its side lengths equal to b and a(<<b). In the plane of the loop there is another very small loop A in shape of a square of side length x. Loop A is placed symmetrically with respect to B with its centre at a distance a from one of its longer side (see Figure). There is a current (i) in loop A which is made to increase at a constant rate of didt=αAs–1. Calculate the emf induced in the bigger loop.
View SolutionA rectangular conducting loop of length l and breadth b enters a uniform magnetic field B as shown below.
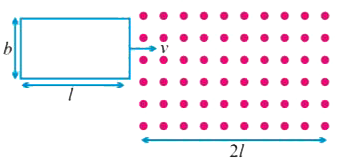
The loop is moving at constant speed v and at t = 0 it just enters the field B. Sketch the following graphs for the time interval t = 0 to t=3lv.
(iii) Power versus time
Resistance of the loop is R.
View SolutionFig. 6.50 shows a rectangular conducting loop PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a velocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for the current in the loop (ii) the force and (iii) the power required move the arm PQ.
View SolutionA circular conducting loop of radius r0 and having resistance per unit length λ as shown in the figure is placed in a magnetic field B which is constant in space and time. The ends of the loop are crossed and pulled in opposite directions with a velocity v such that the loop always remains circular and the radius of the loop goes on decreasing, then

View Solution
