A: When the magnetic flux through a loop is maximum, induced emf is maximum.
R: When the magnetic flux through a loop is minimum, induced emf is minimum.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion.
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion.
If Assertion is true statement but Reason is false.
If both Assertion and Reason are false statements.
The correct Answer is:D
To solve the given question, we need to analyze the assertion (A) and the reason (R) provided.
Step 1: Analyze Assertion (A)
The assertion states: "When the magnetic flux through a loop is maximum, induced emf is maximum."
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes, and it can change over time.
- According to Faraday's law of electromagnetic induction, the induced emf (ε) in a loop is proportional to the rate of change of magnetic flux through the loop:
ϵ=−dΦdt
- If the magnetic flux is at a maximum and not changing (i.e., it is constant), then the rate of change of flux (dΦ/dt) is zero. Therefore, the induced emf will also be zero.
Conclusion for A: The assertion is incorrect.
Step 2: Analyze Reason (R)
The reason states: "When the magnetic flux through a loop is minimum, induced emf is minimum."
- Similar to the previous analysis, if the magnetic flux is at a minimum and remains constant, then again the rate of change of flux (dΦ/dt) is zero.
- This means that the induced emf will also be zero when the flux is constant, regardless of whether it is at a maximum or minimum.
Conclusion for R: The reason is also incorrect.
Step 3: Final Conclusion
Since both the assertion (A) and the reason (R) are incorrect, the correct option is that both statements are wrong.
Final Answer:
Both A and R are incorrect.
---
The assertion states: "When the magnetic flux through a loop is maximum, induced emf is maximum."
- According to Faraday's law of electromagnetic induction, the induced emf (ε) in a loop is proportional to the rate of change of magnetic flux through the loop:
ϵ=−dΦdt
- If the magnetic flux is at a maximum and not changing (i.e., it is constant), then the rate of change of flux (dΦ/dt) is zero. Therefore, the induced emf will also be zero.
The reason states: "When the magnetic flux through a loop is minimum, induced emf is minimum."
- This means that the induced emf will also be zero when the flux is constant, regardless of whether it is at a maximum or minimum.
Since both the assertion (A) and the reason (R) are incorrect, the correct option is that both statements are wrong.
Both A and R are incorrect.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -C) Previous Years Questions
Explore 23 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTEChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION -J(Aakash Challengers Questions)
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
When is the magnetic flux through an area element (i) maximum (ii) zero ?
View SolutionA square loop 10 cm to a side is placed on a wooden table in a uniform magnetic field of magnitude 0.25 T. It is found that the biggest magnetic flux through the loop is measured when the loop is flat on the table. What is the flux through the loop when it is tilted such that the plane of the loop makes a 60° angle with the table?
View Solution
Knowledge Check
To induce an e.m.f. in a coil, the linking magnetic flux
AMust decreaseBCan either increase or decreaseCMust remain constantDMust increaseThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
AIf ϕ=0,e must be 0BIf ϕ≠0,e cannot be 0CIf e is not 0,ϕ may or may not be 0DNone of the above is correctThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
AIf ϕ=E must be 0BIf ϕ≠0 E cannot be zeroCIf E is not 0 ϕ may or may not be 0Dnone of the above is correct
At the Earth's equator, B is horizontal and to the north, with a magnitude of approximately 7×10−5T. (a) What is the magnetic flux through a loop of radius 0.1 m, lying flat on the ground? (b) If the same loop is balanced on its edge such that its axis points northwest, what is the magnetic flux through the loop? (c) If the loop is now rotated such that its axis points north, what is the magnetic flux through the loop? (d) If the loop is now rotated such that its axis points west, what is the magnetic flux through the loop?
View SolutionFor a coil rotating in a uniform magnetic field, in which position of the coil is the emf induced in the maximum? What is the magnetic flux through the coil in this position?
View SolutionAn induced emf is produced when a magnet is plunged into a coil. The magnitude of the induced emf is independent of
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
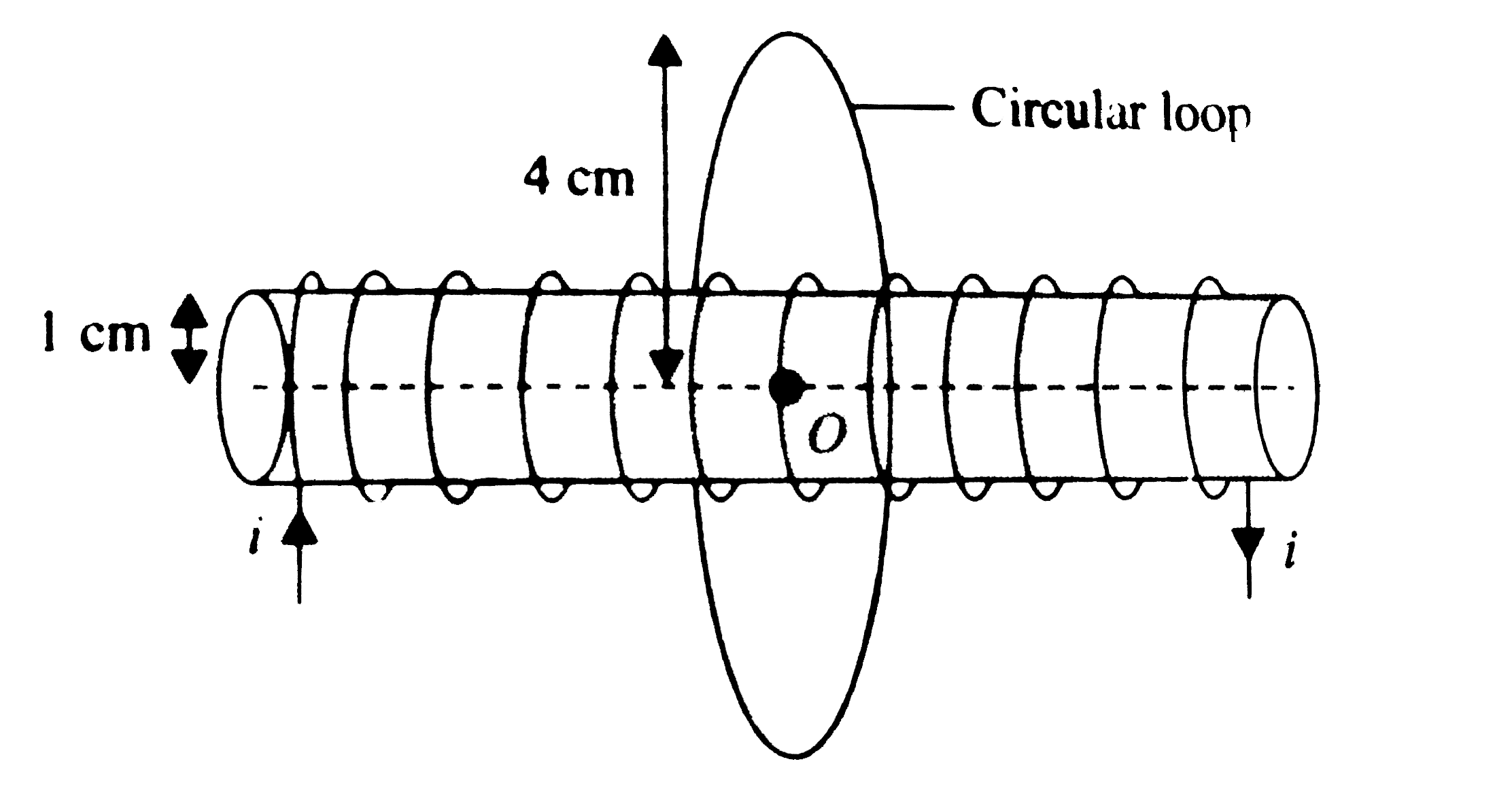
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.
View SolutionIf the magnetic field is doubled through a coil of number of turns 'n' then the induced emf will be
View Solution

