A moan sinms across a river with speed of Vm perpendicular to the flow direction of river. If the water flows with a speed Vw with what resullant velocity does the man cross the river ?
The directions of →vmand→vw are shown in the figure. Using the traingle method. The resultant velocity is given by third side of △AOC , , taken in opposite order.
¯¯¯¯¯¯AC=¯¯¯¯¯¯AO+¯¯¯¯¯¯OC
∣∣¯¯¯¯¯¯AC∣∣=√AO2+OC2 [ using pythogoras therem)
√v2m+v2w
the direction θ the resultant makes with the ¯vm is tanθ=|¯vw||¯vm|
⇒θ=tan−1(|¯vw|)|¯vm|

Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:llustration 1 :
Explore 1 Video
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Try yourself
Explore 48 Videos
- MOCK_TEST_17Book:AAKASH INSTITUTEChapter:MOCK_TEST_17Exercise:Example
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
A river flows at 3 m/s and is 300 m wide . A man swing across the rivers with a velocity of 2 m/s directed always perpendicular to the flow of current . (a) How long does it take the man to cross the river ? (b) In what direction does he actually moves to cross the relative to the shore ? (c) How far down the fiver(from the starting point ) does he reach the opposite bank?
View SolutionA person rows a boat in a water with a speed of 4ms−1. Water in the river is flowing with a speed of 2ms−1 . If the person rows the boat perpendiculat to thedirection of flow, find resultant velcity of the boat and time taken by boat to cross the river if widthe of the river is 400m.
View Solution
Knowledge Check
A man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
AThe minimum time in which he can cross the river is dvBHe can reach the point P in time dvCHe can reach the point P in time d√v2−u2DHe cannot reach P if u>vA man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
AHe can reach the point A in time d/vBHe can reach the point A is time d√v2−u2CThe minimum time in which he can cross river is dvDHe can not reach A if u gt vA boat 'B' is moving upstream with velocity 3m/s with respect to ground. An observer standing on the boat observes that a swimmer 'S' is crossing the river perpendicular to the direction of motion of the boat. If river flow velocity is 4m/s and swimmer crosses the river of width 100,m is 50s. Then
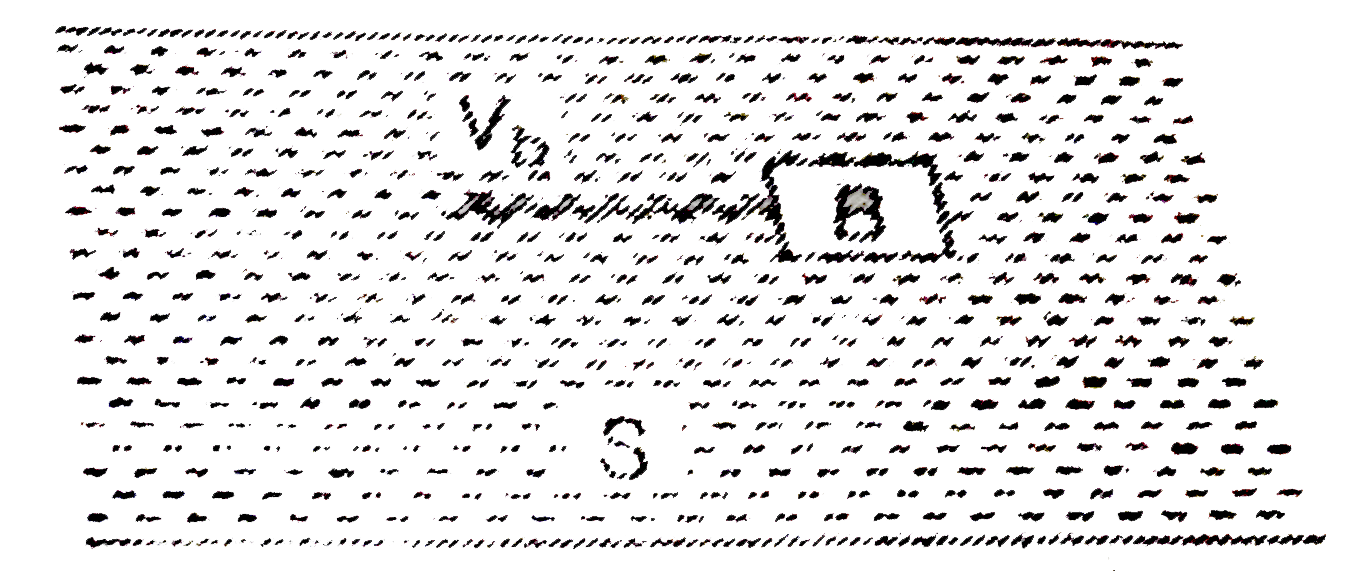 Avelocity of swimmer w.r.t ground is √13m/sBdrift of swimmer along river is zeroCdrift of swimmer along river will be 50mDvelocity of swimmer w.r.t grond is 2m/s
Avelocity of swimmer w.r.t ground is √13m/sBdrift of swimmer along river is zeroCdrift of swimmer along river will be 50mDvelocity of swimmer w.r.t grond is 2m/s
A man swims across a river with speed of 5kmh−1 ( in still water). While a boat goes upstream with speed 12kmh−1 ( in still water). How fast and in which direction does, the man appear to go to the boatman ? Given that the speed of flowing water is 2kmh−1
View SolutionA man swim at an angle θ=120∘ to the direction of water flow with a speed Vmw=5 km/hr relative to water.If the speed of water Vw=3 km/hr, Find the speed of the man.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
View SolutionA boat B is moving in upstream with velocity 3m/s with respect to ground. An observer standing on boat obsserves that a swimmer S is crossing the river perpendicular to the direction of motion of boat. If river flow velocity is 4m/s and swinner crosses the river of width 100m in 50 sec, then
View Solution

