A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
The minimum time in which he can cross the river is
He can reach a point exactly opposite on the bank in time
He cannot reach a point exactly opposite on the bank if
He cannot reach a point exactly opposite on the bank if
The correct Answer is:A, B, C
For minimum time

For reaching a point exactly opposite
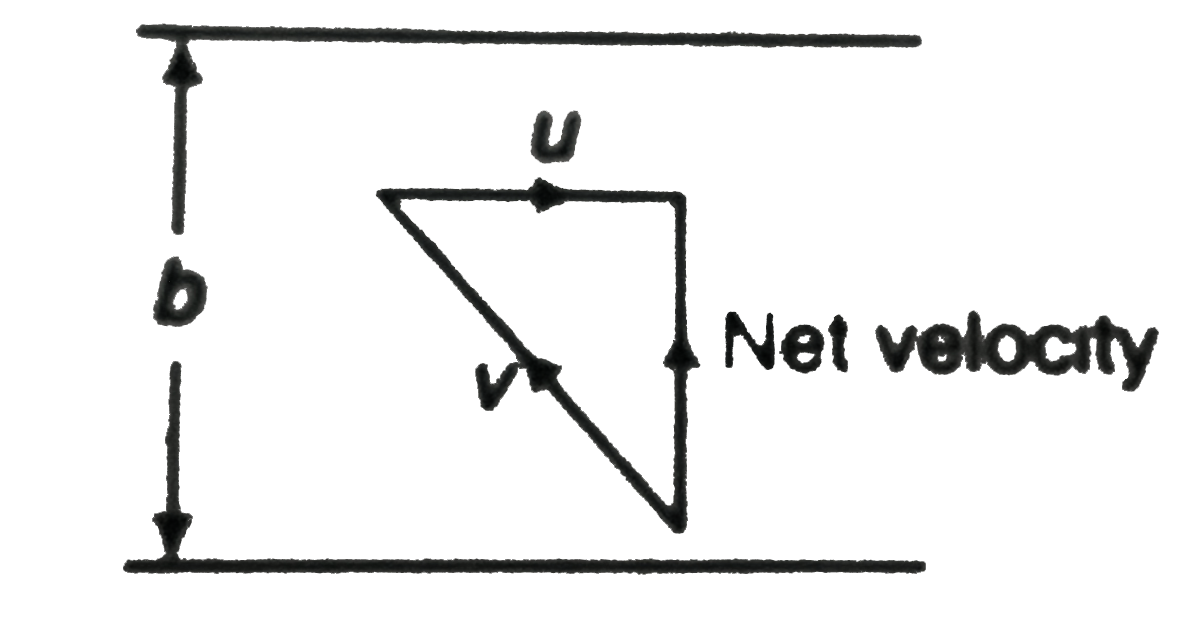
Net velocity=
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Subjective Questions
Explore 24 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Subjective
Explore 51 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A man can swim with velocity v relative to water. He has to cross a river of width d flowing with a velocity u(u>v). The distance through which he is carried down stream by the river is x. Which of the following statements is correct?
View SolutionA man can swim in still water with speed v. He wants to cross a river of width d that flows with speed u and reaches the point directely opposite to his starting point. (a) In which direction should he try to swim (i.e., find the angle the makes with the river flow)? (b) much time will he take to cross the river ?
View Solution
Knowledge Check
A man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
AThe minimum time in which he can cross the river is dvBHe can reach the point P in time dvCHe can reach the point P in time d√v2−u2DHe cannot reach P if u>vA man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
AHe can reach the point A in time d/vBHe can reach the point A is time d√v2−u2CThe minimum time in which he can cross river is dvDHe can not reach A if u gt vA man can swim with velocity v relative to water. He has to cross a river of width d flowing with a velocity u(u>v). The distance traveled by man along the flow is x, when he reaches to opposite bank. For x to be minimum the person should swim at an angle α with the direction of the flow of water, where α is
Asin−1(v/u)Bsin−1(u/v)Cπ2+sin−1(v/u)Dπ2+sin−1(u/v)
A man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow at an angle of 120 with the river flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View SolutionA man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
View SolutionA boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
View SolutionA man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
View SolutionA man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60° with the flow of direction while swimming, The time taken by him to cross the river will be
View Solution

