The speed of a train increases at a constant rate α from zero to v and then remains constant for an interval and finally decreases to zero at a constant rate β. The total distance travelled by the train is l. The time taken to complete the journey is t. Then,
t=l(α+β)αβ
t=lv+v2(1α+1β)
t is minimum when v=√2lαβα−β
t is minimum when v=√2lαβα+β
The correct Answer is:B, D
v=αt1⇒t1=vα
v=βt2⇒t2=vβ
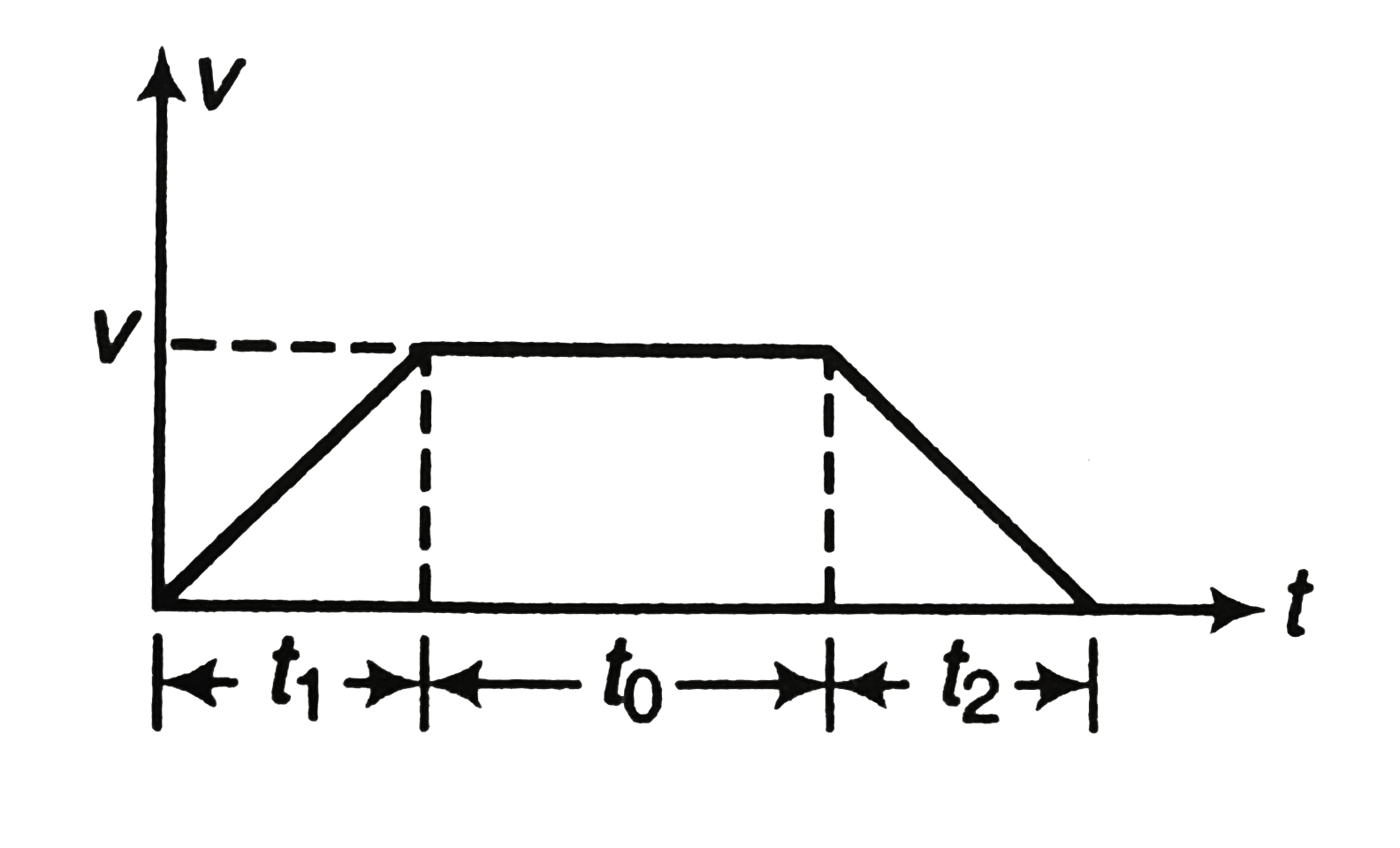
∴t0=t−t1=(t−vα−vβ)
Now, l=12αt21+vt0+12βt22
=12(α)(va)2+v(t−vα−vβ)+12(β)(vβ)2
=vt−v22α−v22β
∴t=lv+v2(lα+1β)
For t to be minimum its first derivation with respect
to velocity be zero or,
0=−lv2+α+β2αβ
∴v=√2lαβα+β
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective
51 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
the velcoity of a trian incrreases at a constant rate α from 0 to v and then remains constant for same interval and then finally decreases to zero at constant rate β.if the total distance coverd by the the particle x,then show that the total time taken will be
txv+v2[1α+1β].
View SolutionA train is travelling between two stations distant s apart. During the first part its speed increases at a constant rate f1 from zero to v, then remains constant for an interval and finally decreases to zero at a constant rate f2. The total time taken is
sv+12v[1f1+1f2]
View Solution
Knowledge Check
A car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
As=172ft2Bs=136ft2Cs=12ft2Ds=14ft2A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
The speed of a car increases uniformly from zero to 10ms−1 in 2s and then remains constant (figure)

a. Find the distance travelled by the car in the first two seconds.
b. Find the distance travelled by the car in the next two seconds.
c. Find the total distance travelled in 4s.
View SolutionA left storing from rest assends with constants acceleration 'a', then with a constant velcoity and finally stops under a constant retardation 'a'. If the total distance assended is 'x' and the total time taken is 't',show that the time during which the left is assending with constant vlocity is
√t2−4xa
View SolutionWhen the speed remains constant, the distance travelled is ______proportional to the time
View SolutionA train accelerates from at the constant rate b for time t2 at a constant rate a and then it retards at the comes to rest. Find the ratiot1//t2.
View SolutionA car,starting from rest, accelerates at the rate f through a distance s, then continuous at constant speed for time t and then decelerates at the rate f2 come to rest. If the total distance traversed is 5 s,then :
View SolutionA lift ascends with constant acceleration a=1ms−2, then with constant velocity and finally, it stops under constant retardation a=1ms−2. If total distance ascended by the lift is 7 m, in a total time of the journey is 8 s. Find the time (in second) for which lift moves with constant velocity.
View Solution
