A tunnel is made across the earth at disance R2 from the centre of eath. A particle is dropped (from rest) in the tunnel at one end. If v1 is the speed of particle when passing through the centre of tunnel and v2 is the orbital speed of an earth satellite (very close to earth's surface). If v1y2=√x+1x. Find the value of x.
The correct Answer is:2
Step by step video, text & image solution for A tunnel is made across the earth at disance (R )/(2) from the centre of eath. A particle is dropped (from rest) in the tunnel at one end. If v_(1) is the speed of particle when passing through the centre of tunnel and v_(2) is the orbital speed of an earth satellite (very close to earth's surface). If (v_(1))/(y_(2))=(sqrt(x+1))/(x). Find the value of x. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
5 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -I (Subjective Type Question)
9 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
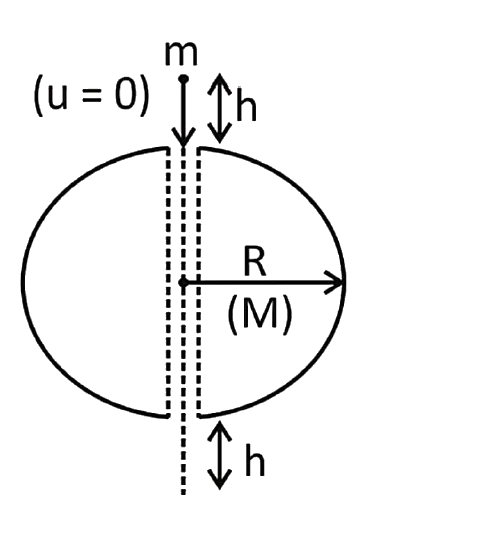
View Solution
Knowledge Check
A tunnel is made inside earth passing throgh centre of earth. A particle is dropped from the surface of earth. Select the correct statement :
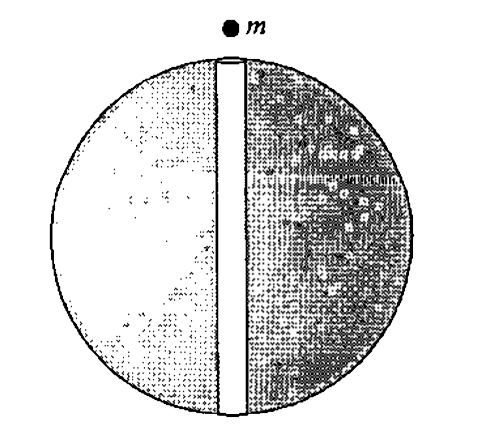 AKinetic energy of particle is maximum at centre and its potential energ is zero at centerBVelocity of particle is proportional to x [where x is distance of particle from center of earthCKinetic energy of particle is maximum when it reaches on the other side of tunnelDKinetic energy of particle is maximum at center
AKinetic energy of particle is maximum at centre and its potential energ is zero at centerBVelocity of particle is proportional to x [where x is distance of particle from center of earthCKinetic energy of particle is maximum when it reaches on the other side of tunnelDKinetic energy of particle is maximum at centerA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth ve is :
Ave2BveC√2veDve√2A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
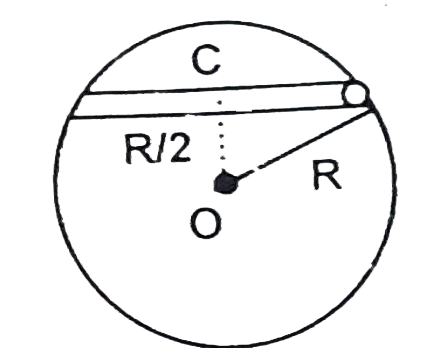 A√3GM2RB√3GM4RC√3GM8RDd√3GM16R
A√3GM2RB√3GM4RC√3GM8RDd√3GM16R
Two satellites S1 and S2 revolve around the earth at distances 3R and 6R from the centre of the earth. Find the ratio of their (a) linear speeds and (b) angular speeds.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View SolutionA tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionA tunnel is dug along a diameter of the planet. A particle is dropped into it at the surface. The particle reaches the centre of the planet with speed v. If ve is the escape velocity from the surface fo the planet, then-
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View Solution
