A force -F is applied at the topmost point of a cylinder of radius r and height h.
(a) If the cylinder remains at rest, then find distance of line of action of normal reaction from center of mass.
(b) Find coefficient of friction required so that the cylinder tooples before sliding.
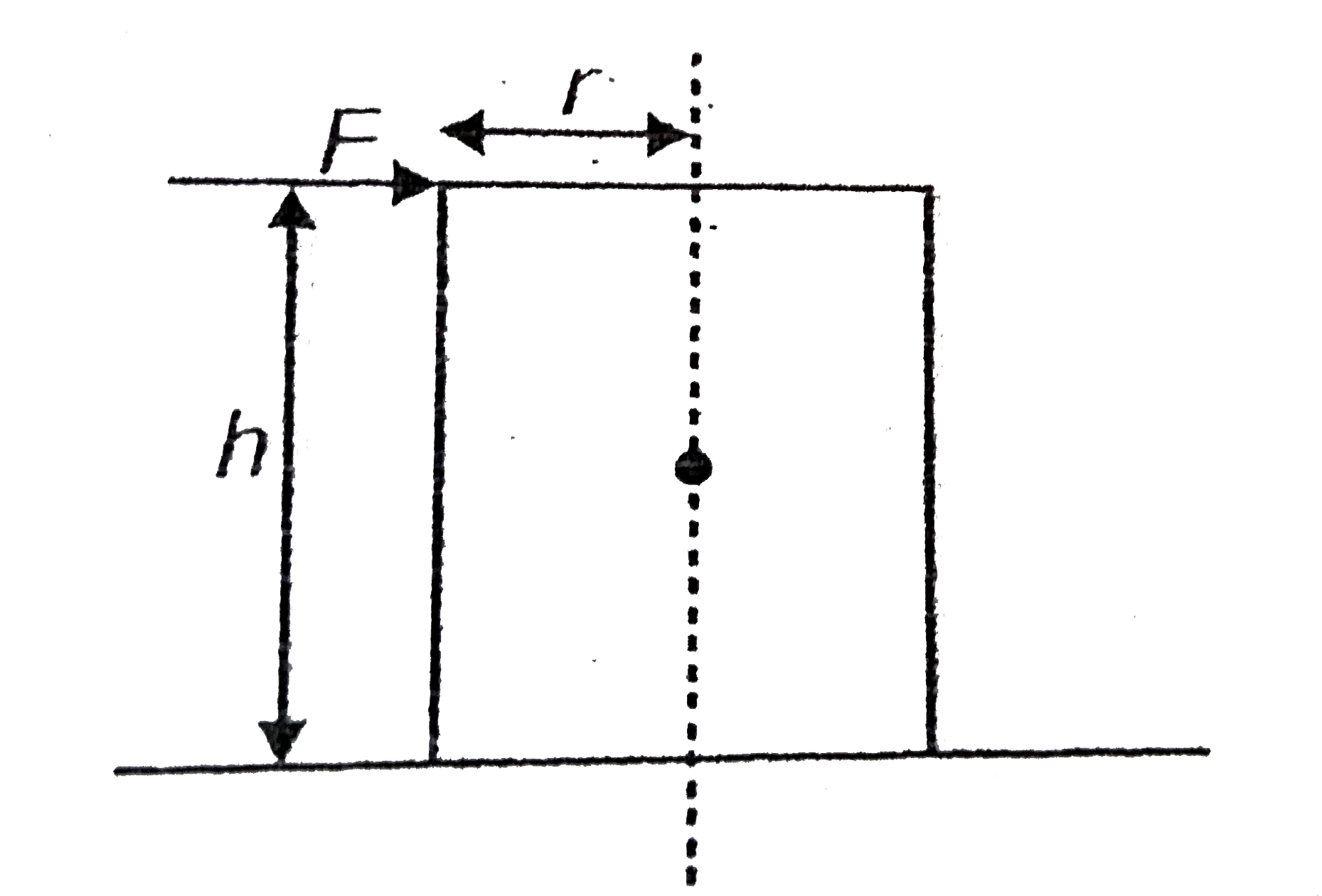
(a) 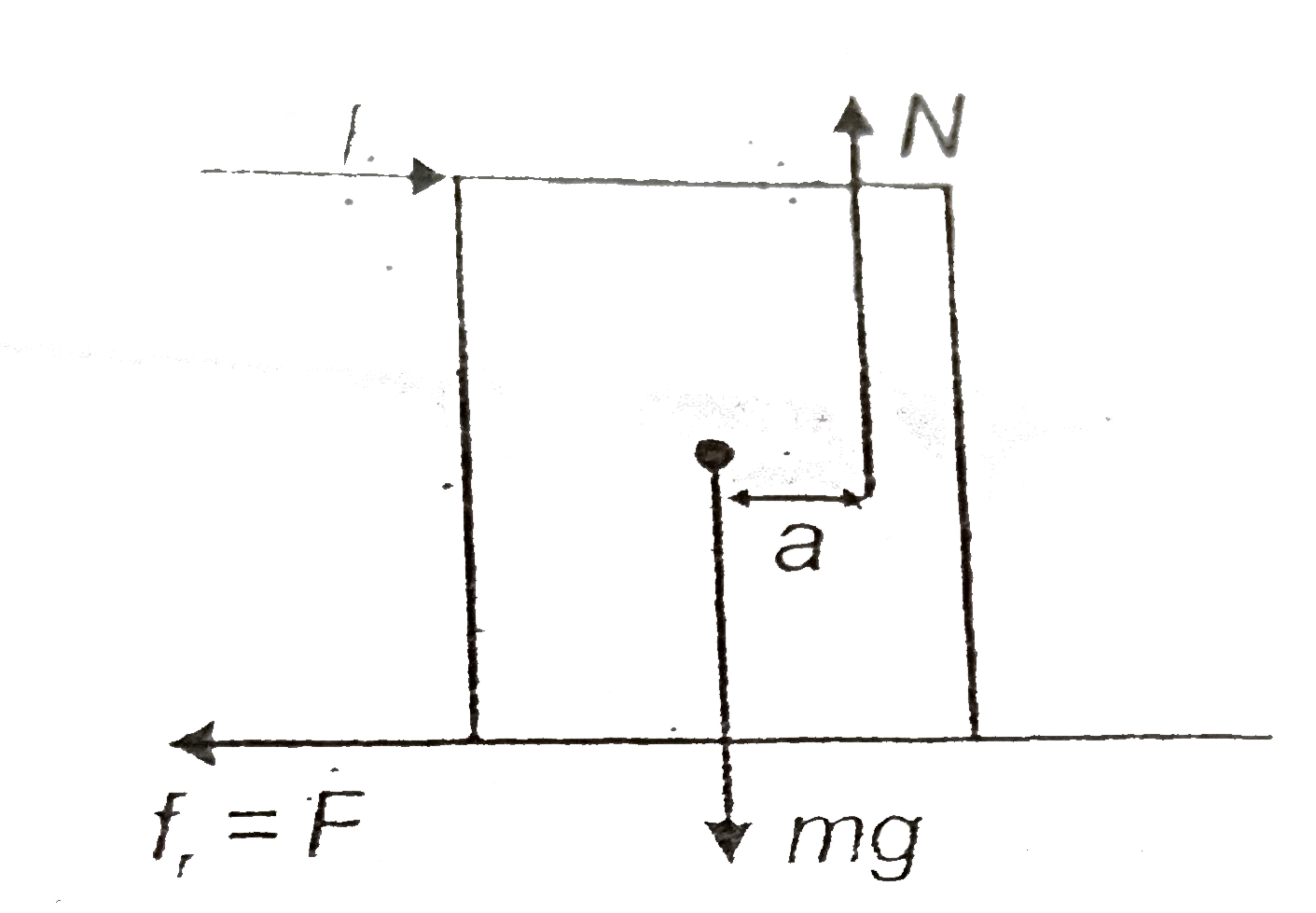
Since body is at rest, it is in translational equilibrium
fr=F
For rotational equilibrium,
τnet=0 (about center)
⇒F×h2+F×h2−Na=0 (∵fr=F)
⇒a=F⋅hN=F⋅hmg
(b) 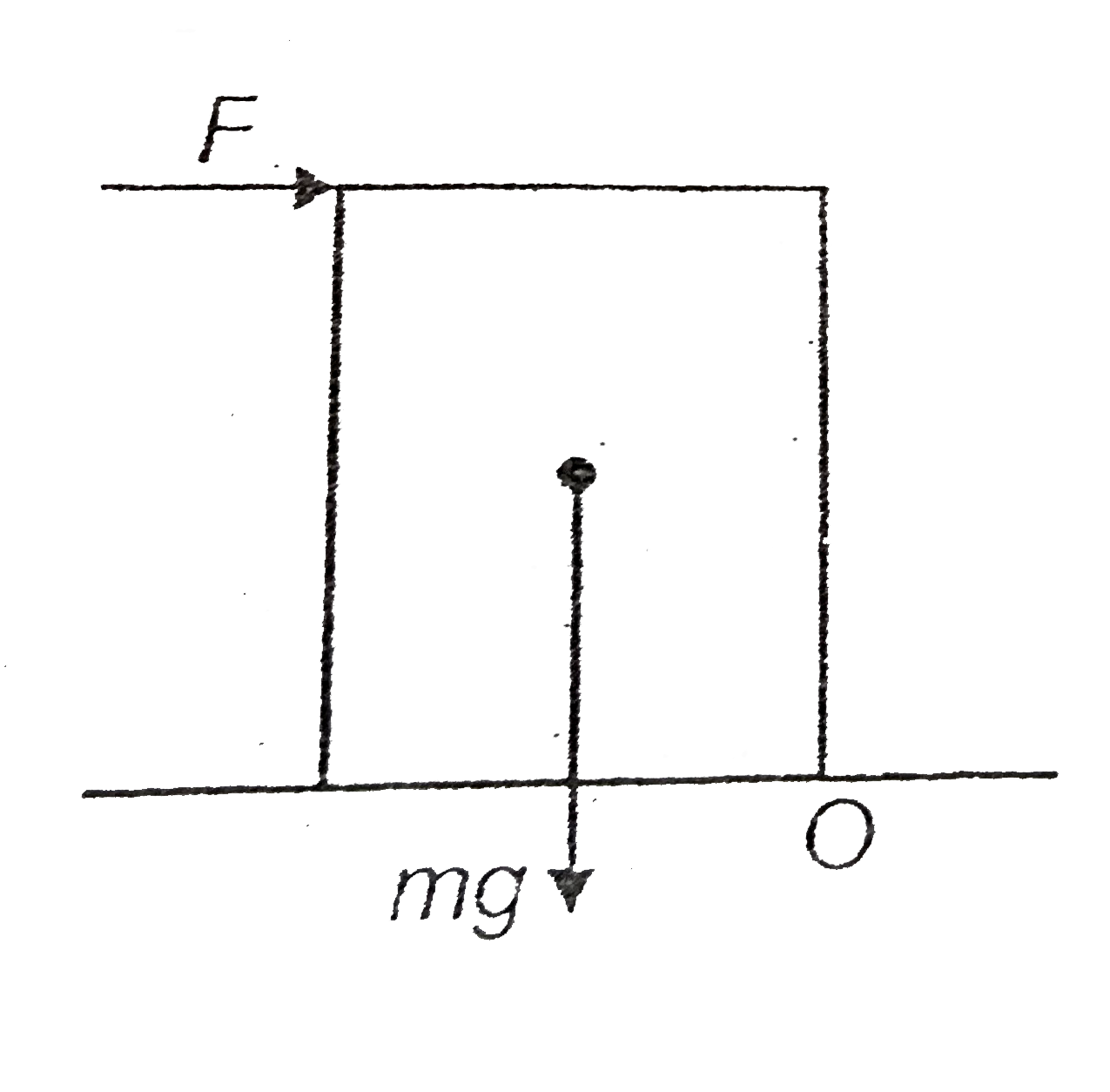
For toppling about point O,
τF>τmg
⇒F.h>mg.r
⇒F>mgrh
To avoid sliding, F<μmg
Therefore, mgrh<F<μmg
⇒rh<μ
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
A force F acts tangentially at the highest point of a solid cylinder of mass m kept on a rough horizontal plane. If the cylinder rolls without slipping, find the acceleration of the center of cylinder.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
Knowledge Check
The moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
A12M(a2+2b2)B12M(2a2+b2)C12M(a2+b2)D12M(a23+b212)A solid cylinder of radius r and height h is melted and casted into a cone. If radius of cone is (r2) then find its height.
A4 hB6 hC12 hD8 hA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
 Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Radius of a cylinder is r and the height is h. Find the change in the volume if the
height is doubled.
View SolutionIf radius is r and height is h, then find curved surface area of cylinder.
View SolutionA uniform cylinder of radius r and radius of gyration is kept on a fixed wedge of inclination θ. When we push the wedge with a constant acceleration a, the cylinder rolls up the wedge. Find coefficient of friction between the cylinder and wedge.

View SolutionRadius of a cylinder is r and the height is h. Find the change in the volume if the
height is doubled and the radius is halved.
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
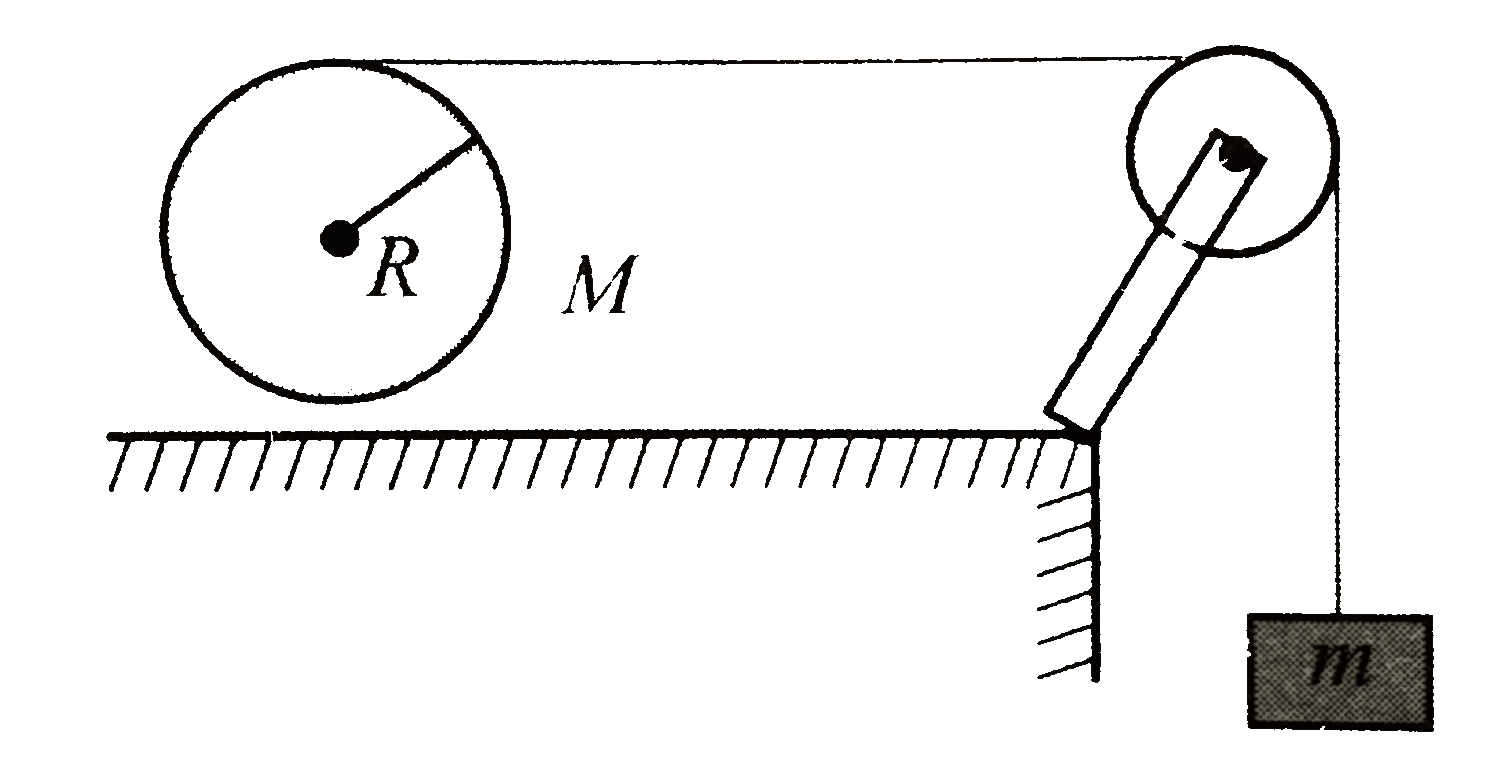
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View Solution