A uniform cylinder of radius r and radius of gyration is kept on a fixed wedge of inclination θ. When we push the wedge with a constant acceleration a, the cylinder rolls up the wedge. Find coefficient of friction between the cylinder and wedge.

Let us push the wedge with a force F such that it moves with an acceleration a, as shown in figure. Now we can impose a pseudo force ma acting on the cylinder to write the force equation relative to the accelerating frame (wedge).
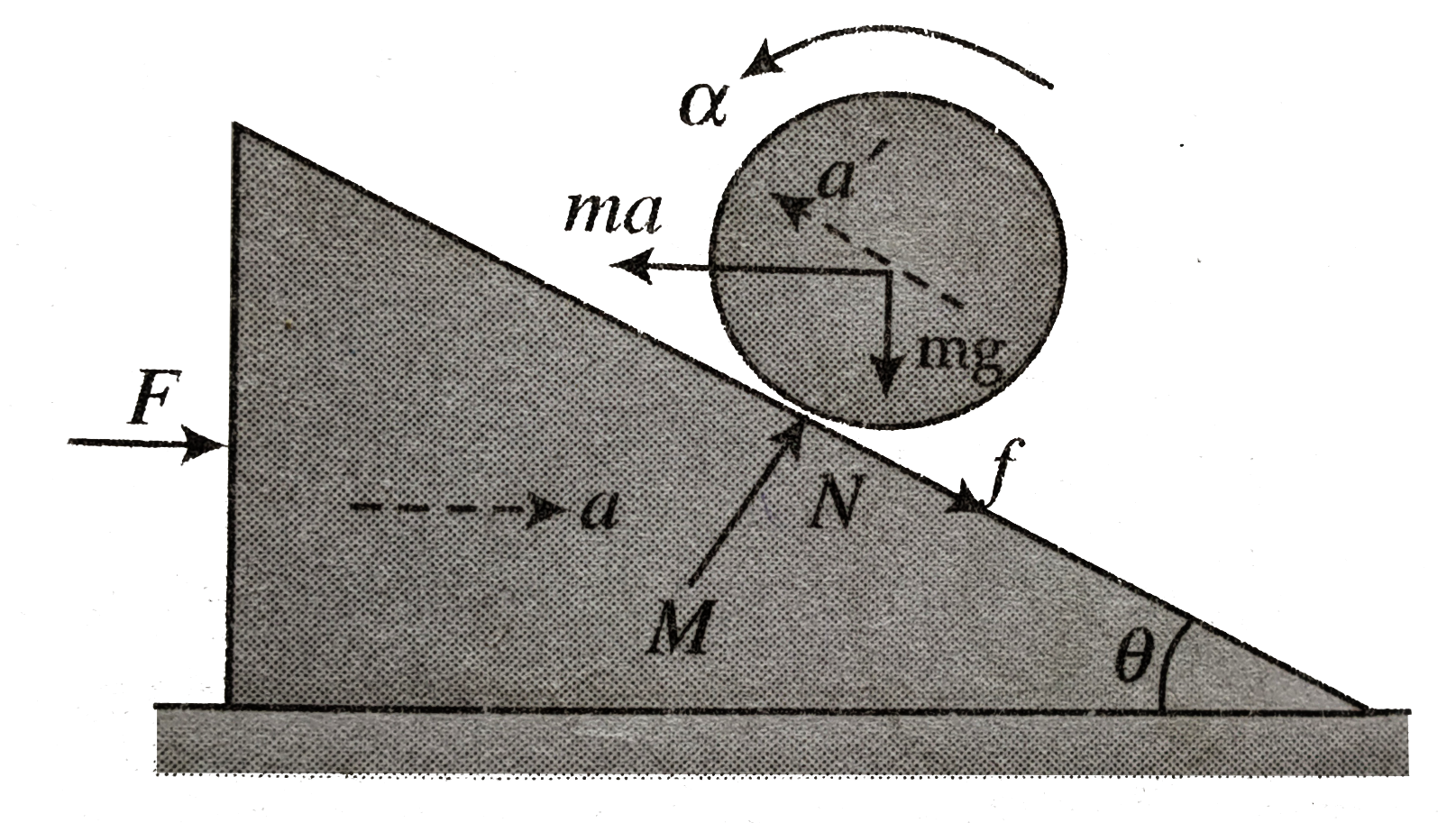
Let us assume that the cylinder rolls up with acceleration a––' relative to the wege. Hence, the friction of will point down the incline of the wedge.
Force equation , For m
macosθ−mgsinθ−f=ma'............i
For m:mgcosθ+masinθ=N..........ii
Torque equation
For m:=mk2α .............iii
Equation of rolling of m:a'=rα ...........iv
Law of static friction : f≤μN .............v
Eliminating α eqn iii by substituting a'=rα from eq iv we have f=mk2r2a'
Substituting a'=fr2mk2 in eqn i we have
f=macosθ−mgsinθ(1+r2k2)
Now substituting f from the above equation and N from eq ii in eq v we have
μ≥acosθ−gsinθ(1+r2k2)(asinθ+gcosθ)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check

A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of these
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?AF/4BF/3CF/2D2F/3A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
In figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
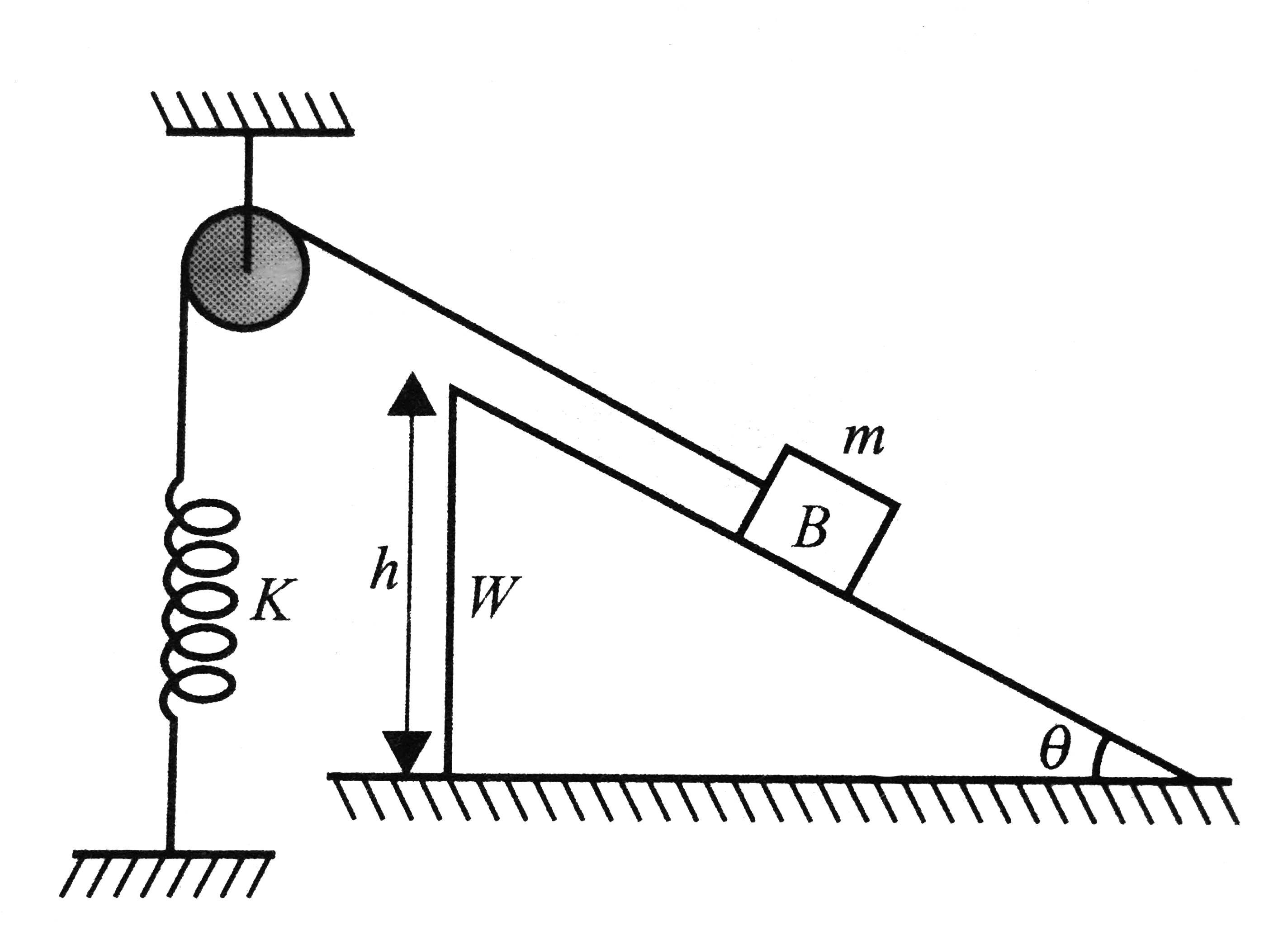
View SolutionIn the figure shown the pulley is smooth . The spring and the string are light. The block 'B' slides down from the top along the fixed rought wedge of inclination θ. Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and the spring was relaxed when the block was relased from the top of the wedge.
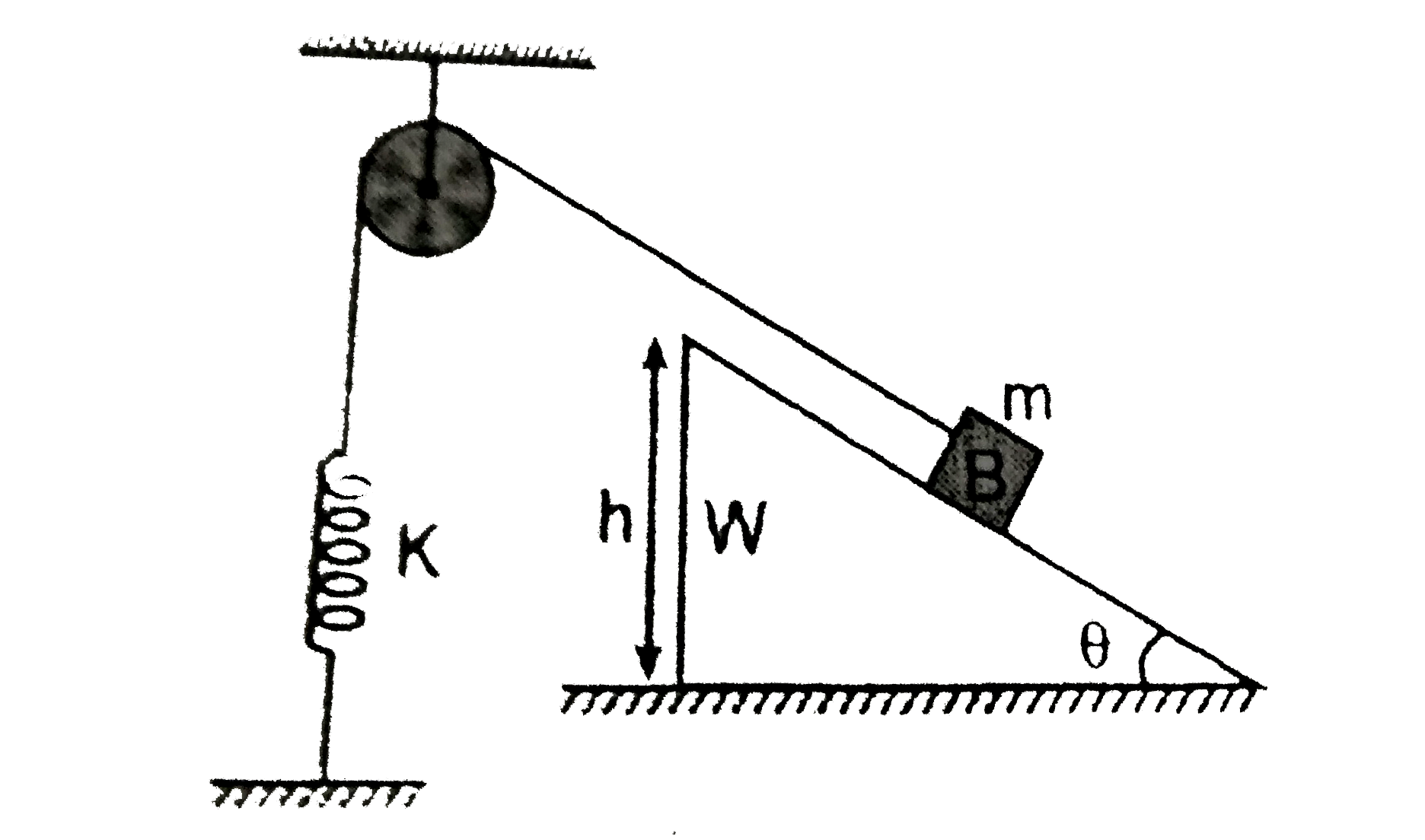
View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View SolutionA block of mass m is lying on a wedge having inclination angle α=tan−1(15) wedge is moving with a constant acceleration a=2ms−2 The minimum value of coefficient of friction μ so that m remain stationary w.r.t. wedge is

View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
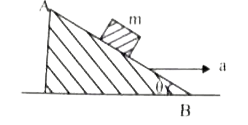
View Solution

