A force F acts tangentially at the highest point of a solid cylinder of mass m kept on a rough horizontal plane. If the cylinder rolls without slipping, find the acceleration of the center of cylinder.
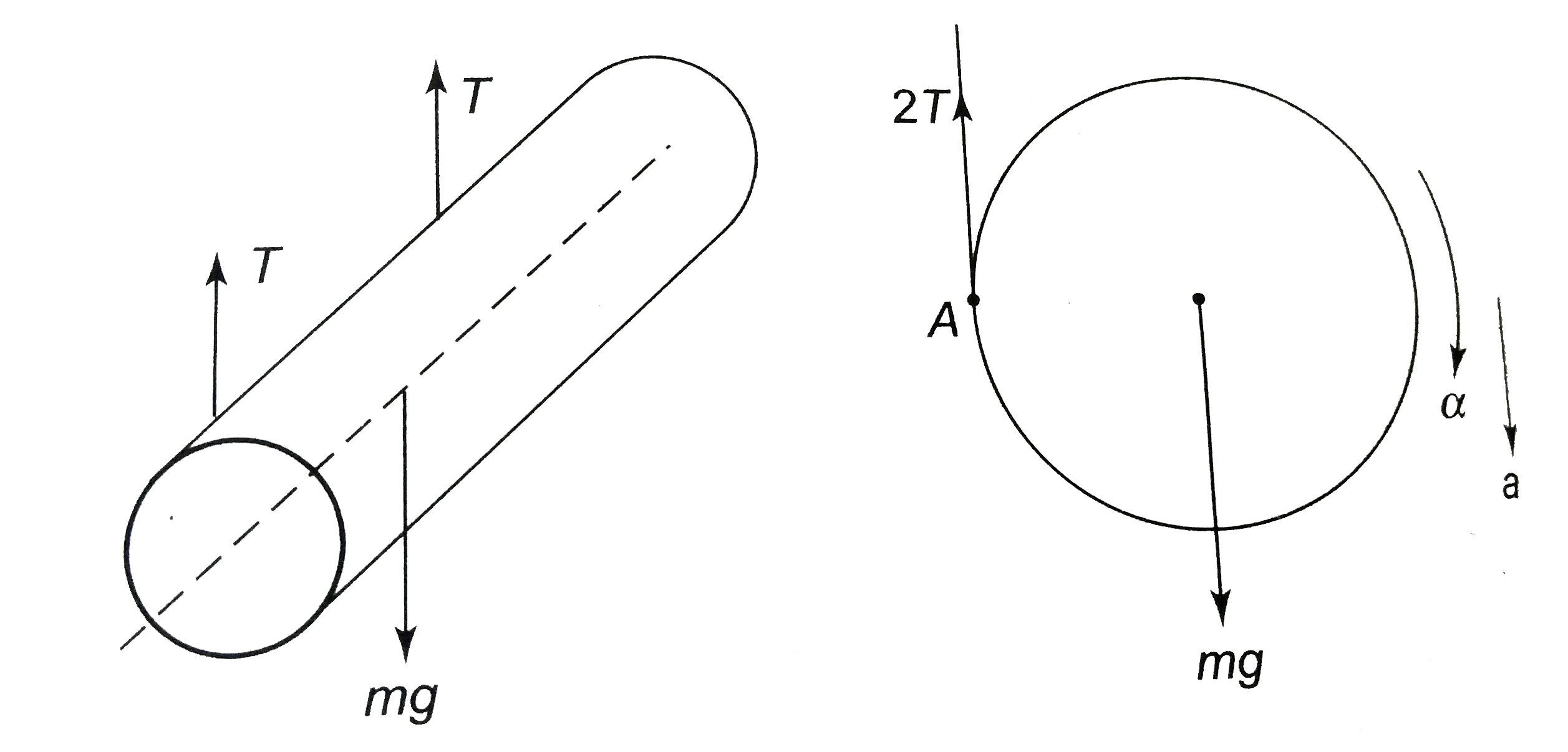
Linear motion: mg−2T=ma (i)
Rotational motion: 2T⋅R=Ic.m.α=12mR2α (ii)
a=Rα (iii)
From (ii), T=14mRα=14ma⇒ma=4T in (i)
mg−2T=4T⇒T=mg6
T=14mRα⇒mg6=14mRα⇒2g3R
a=Rα=2g3
Linear velocity of cylinder after time t
v=at=2gt3
Power delivered by gravitational force
P=m→g⋅→v=mgv=2mg2t3
Tension=mg6
Angular acceleration =2g3R
Power =2mg2t3
OR
Here the cylinder rolls without slipping on vertical surface
a=gsinθ1+k2R2=gsin90∘1+12=23g
Topper's Solved these Questions
Similar Questions
A force F acts tangentially at the highest point of a sphere f mass m kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of the centre of the sphere.

View SolutionA force F acts tangentially at the highest point of a sphere of mass m kept on a rough horiozontal plane. If the sphere rolls withut slipping, find the accelerastioni of the centre of the sphere.
View Solution
Knowledge Check
A force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 A2F3mB10F7mCzeroD4F3m
A2F3mB10F7mCzeroD4F3mThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
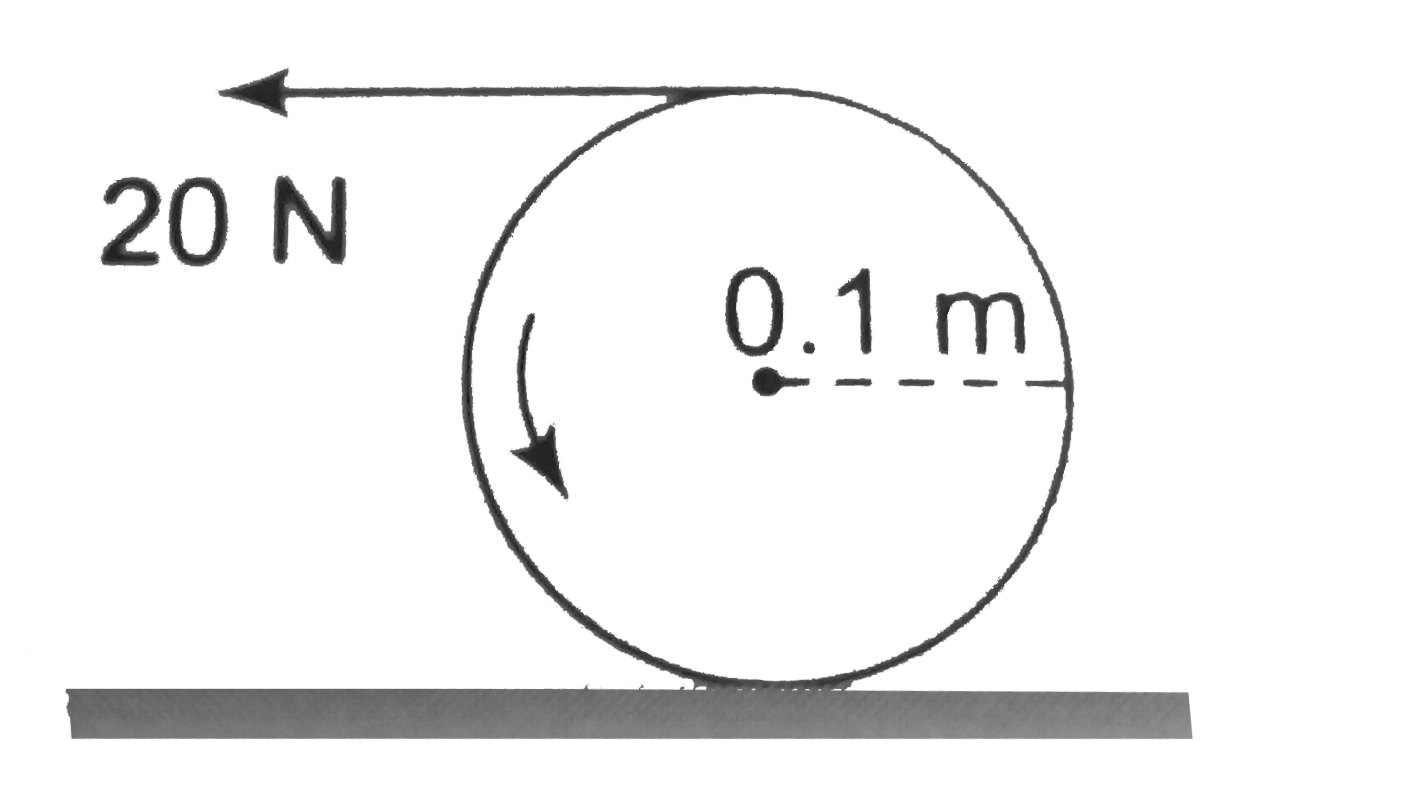 .A6.7m/s2B10.0m/s2C3.3m/s2Dnone of these
.A6.7m/s2B10.0m/s2C3.3m/s2Dnone of theseA cylinder rolls down an inclined plane of inclination 30∘, the acceleration of cylinder is
Ag3BgCg2D2g3
A tangential force 'F' is applied at the topmost point of a spherical shell of mass 'm' kept on a rough horizontal surface. If it rolls without slipping, it's acceleration is 6Fxm then 'x'
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA horizontal force F is applied at a height h above the center of a solid cylinder of mass m and radius R. Determine friction, if cylinder rolls without slipping. For what value of h, friction is zero.
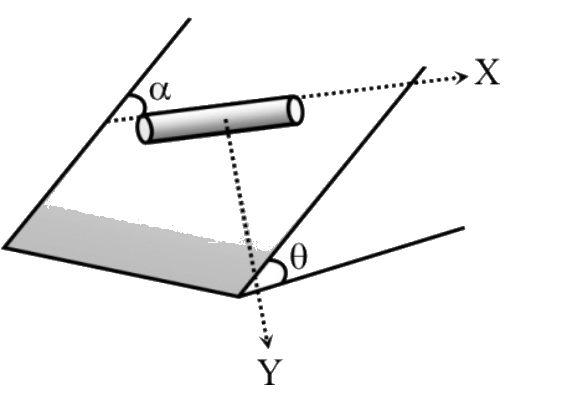
View SolutionA cylinder of mass m is kept on an inclined plane haivng an angle of inclination 30∘. Axis of the cylinder makes an angle 30∘ with the line along the greatest slope. Assuming that cylinder rolls without slipping, the acceleration of the cylinder is
View Solution

