Figure shows a block of mass 'm' resting on a smooth horizontal surface. It is connected to a rigid wall by a massless spring of stiffness 'k'. The spring is in its natural length. A constant horizontal force F starts acting on the block towards right. Find (i) speed of the block as it moves throught a distance x, (ii) speed when the block is in equlibrium and (iii) maximum extension produced in the speing.
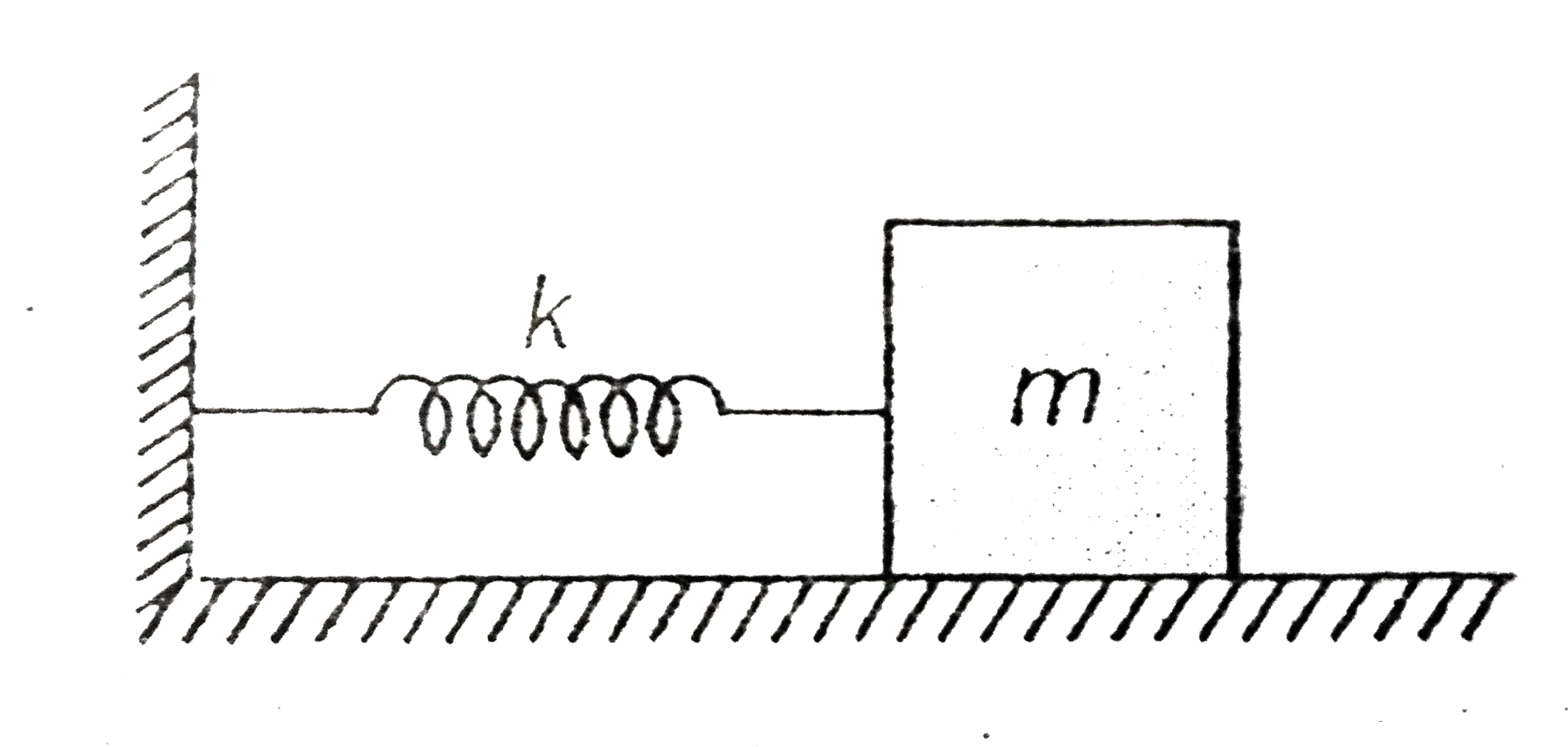
When the block has moved through 'x' its speed is v(say)

The FDB of the block in this situation is shown
(i) By work energy principle, W=ΔK
WF+Wsp=12mv2−0
⇒Fxxxcos0∘−x∫0kxdx=12mv2
⇒fx−12kx2=12mv2
∴v=√2Fx−kx2m
(ii) At equlibrium, net force is zero.
F=kxorx=Fk
Now v=√(2Fx−kx2)m
∴v=
⎷2F2k−F2km=F√mk
(iii) At the maximum extension, speed of the block becomes zero. ∴v=0
or,√2Fx−kx2m=0⇒x=2Fk
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View Solution
Knowledge Check
The figure shown a mass m on frictionless surface It is connected to rigid wall by the mean of a massless spring of its constant K. Initially , The spring at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is x, will be
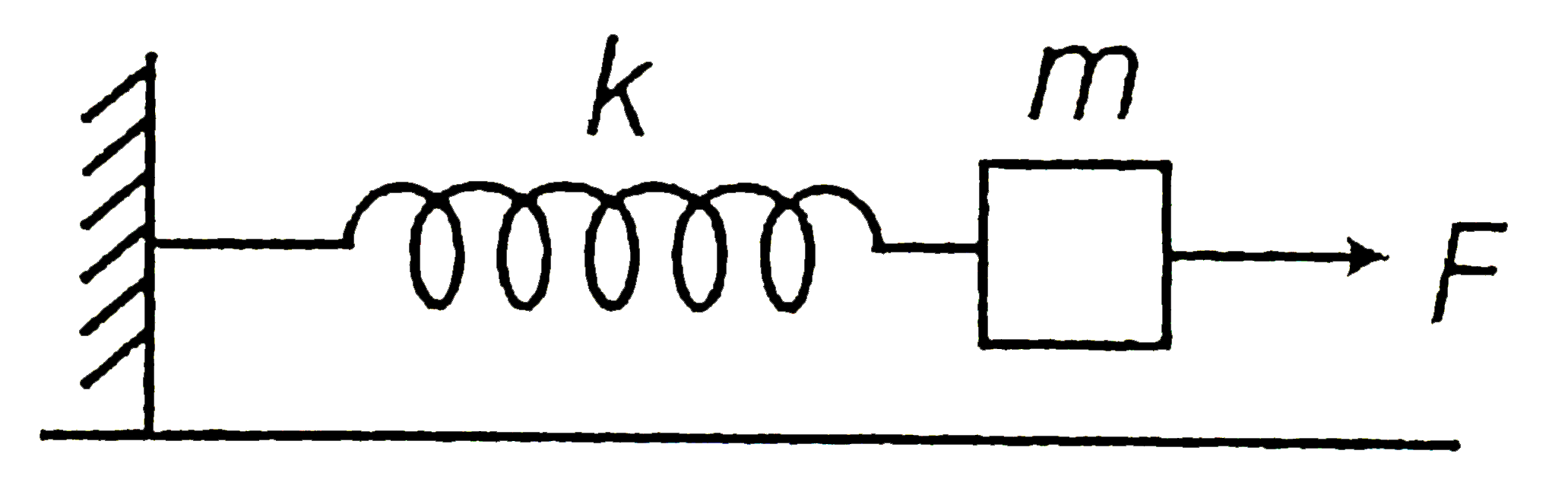 A√2Fx−Kx2mB√Fx−Kx2mC√x(F−K)mD√Fx−Kx22m
A√2Fx−Kx2mB√Fx−Kx2mC√x(F−K)mD√Fx−Kx22mA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionTwo blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time.

View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
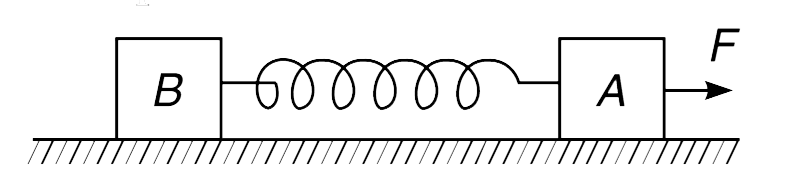
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring

View Solution

