Two blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time.

The correct Answer is:xA=0.12sin(10t)+0.8t
Step by step video, text & image solution for Two blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 39videos
SIMPLE HARMONIC MOTION
- BOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS159videos
ROTATIONAL MOTION
- BOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension33videos
SURFACE TENSION
Similar Questions
The blockA(2kg) and B(3kg) rest up on a smooth horizontal surface are connected by a spring of stiffness 120N/m. Identially the spring is underformd. A is imparted a velocity of 2m/s along the line of the spring away from B. Find the displacement of A at t seconds later.
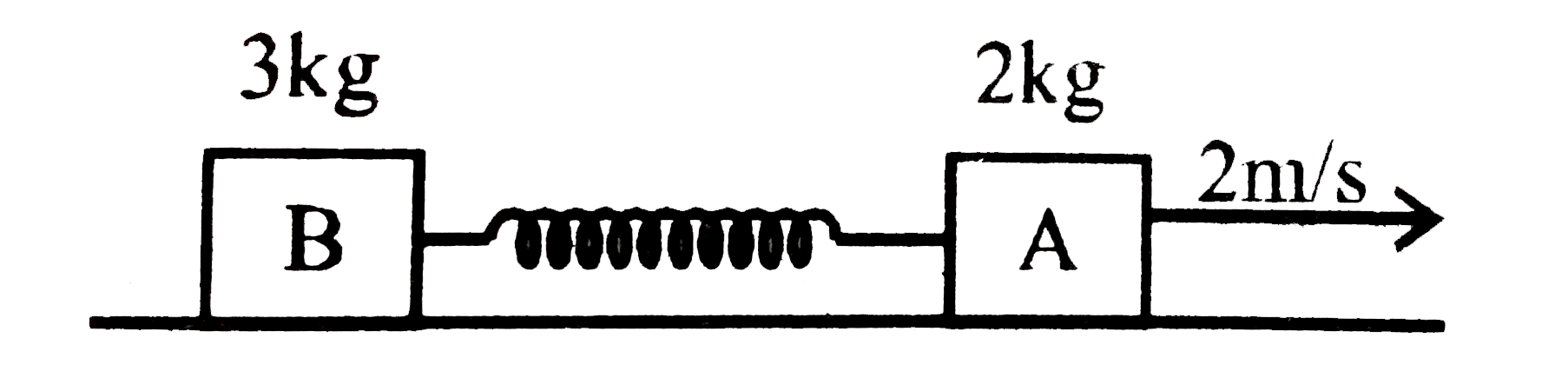 View Solution
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
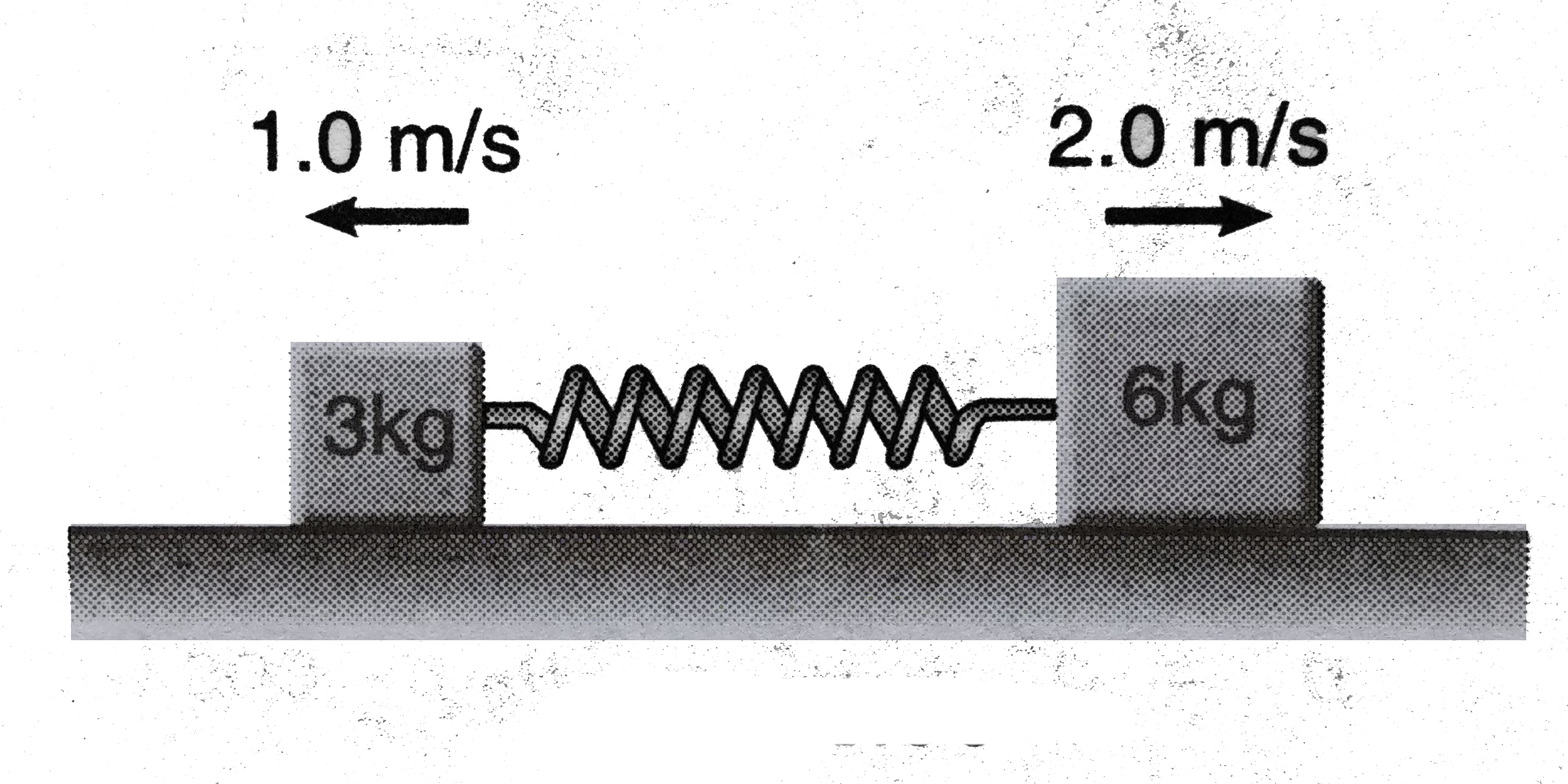 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
A110B12√10C12√15D0.15 - Question 2 - Select One
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cm - Question 3 - Select One
Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of springAzeroBF(m1+m2)m1m2CFm1DFm1+m2
Two blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.
 View Solution
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a massless spring of spring constant K. This system lies over a smooth horizontal surface. At t=0 the bolck A has velocity u towards right as shown while the speed of block B is zero, and the length of spring is equal to its natural length at that at that instant.

Column IColumn II(A)The velocity of block A(P)can never be zero(B)The velocity of block B(Q)may be zero at certain instants of time(C)The kinetic energy of system of two block(R)is minimum at maximum compression of spring(D)The potential energy of spring(S)is maximum at maximum extension of springView SolutionTwo blocks A(3kg) and B(6kg) are connected by a spring of stiffness 512 N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. Velocities 1.8m/s and 2.2 m/s are imparted to A and B in opposite direction. The maximum extension in the spring will be –
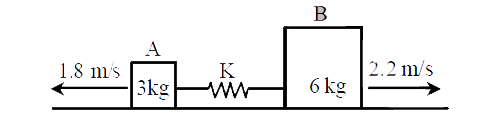 View Solution
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.View Solution

