The reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
a∝v3
a∝v2
a∝v4
a∝v
The correct Answer is:A
To find the relationship between velocity v and acceleration a for a particle moving along the x-axis with the given time-position relation t=px2+qx, we will follow these steps:
Step 1: Differentiate the time-position relation
Given:
t=px2+qx
We differentiate both sides with respect to time t:
dtdt=ddt(px2+qx)
This simplifies to:
1=ddt(px2)+ddt(qx)
Step 2: Apply the chain rule
Using the chain rule, we have:
ddt(px2)=p⋅2x⋅dxdt=2pxv
ddt(qx)=q⋅dxdt=qv
Thus, the equation becomes:
1=2pxv+qv
Step 3: Solve for x
Rearranging the equation gives:
2pxv+qv=1
Factoring out v:
v(2px+q)=1
Now, we can solve for x:
2px+q=1v
2px=1v−q
x=1−qv2pv
Step 4: Differentiate the velocity to find acceleration
Now we need to find acceleration a, which is the derivative of velocity v with respect to time t:
a=dvdt
We differentiate the expression for v with respect to t:
Using v(2px+q)=1, we differentiate both sides:
ddt(v(2px+q))=0
Using the product rule:
dvdt(2px+q)+vddt(2px+q)=0
Step 5: Differentiate 2px+q
Now we differentiate 2px+q:
ddt(2px+q)=2p(dxdt)=2pv
Substituting back into the equation:
dvdt(2px+q)+v(2pv)=0
Step 6: Substitute x back into the equation
Substituting x=1−qv2pv into the equation:
dvdt(2p(1−qv2pv)+q)+2pv2=0
Step 7: Simplify the equation
After simplification, we will find a relationship between a and v:
a=−2pvq
Conclusion
Thus, the relationship between acceleration a and velocity v is:
a∝−v
Given:
t=px2+qx
dtdt=ddt(px2+qx)
1=ddt(px2)+ddt(qx)
Using the chain rule, we have:
ddt(px2)=p⋅2x⋅dxdt=2pxv
ddt(qx)=q⋅dxdt=qv
1=2pxv+qv
Rearranging the equation gives:
2pxv+qv=1
Factoring out v:
v(2px+q)=1
2px+q=1v
2px=1v−q
x=1−qv2pv
Now we need to find acceleration a, which is the derivative of velocity v with respect to time t:
a=dvdt
Using v(2px+q)=1, we differentiate both sides:
ddt(v(2px+q))=0
dvdt(2px+q)+vddt(2px+q)=0
Now we differentiate 2px+q:
ddt(2px+q)=2p(dxdt)=2pv
dvdt(2px+q)+v(2pv)=0
Substituting x=1−qv2pv into the equation:
dvdt(2p(1−qv2pv)+q)+2pv2=0
After simplification, we will find a relationship between a and v:
a=−2pvq
Thus, the relationship between acceleration a and velocity v is:
a∝−v
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - D)
24 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
The relation between time t and distance x for a moving body is given as t=mx2+nx, where m and n are constants. The retardation of the motion is : (When v stands for velocity)
View SolutionThe position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View Solution
Knowledge Check
Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
AVelocity (i.edxdt) of particleBInitial velocity(i.edxdt att=0)CVelocity at t=2secDAccleration(i.ed2xdt2) of particleThe position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle isA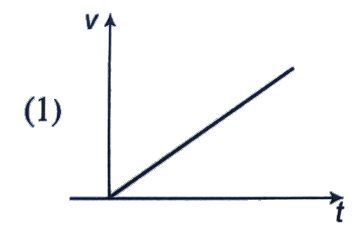 B
B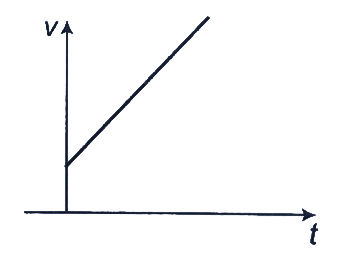 C
C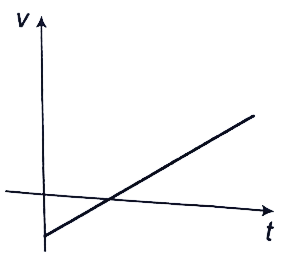 D
D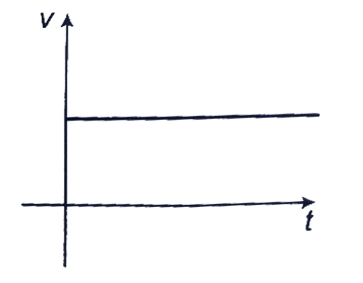
The relation between time t and distance x is t=ax2+bx where aandb are constants. The acceleration is
A2bv3B2av3C−2av2D−2av3
The relation between the acceleration a and displacement x of a particle executing S.H.M. is a=−(p/q)y, where p and q are constants. What will be the time period T of the particle ?
View SolutionThe relation between time t and distance x is t=ax2+bx where aandb are constants. The acceleration is
View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionIf the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
View Solution
