A body starts from rest with an acceleration 2m/s2 till it attains the maximum velocity then retards to rest with 3m/s2. If total time taken is 10 second, then maximum speed attained is
12 m/s
8 m/s
6 m/s
4 m/s
The correct Answer is:A
To solve the problem step by step, we will break it down into parts based on the motion of the body.
Step 1: Understanding the Motion
The body has two phases of motion:
1. Acceleration Phase: The body accelerates from rest with an acceleration of 2m/s2 until it reaches its maximum velocity vmax.
2. Retardation Phase: The body then decelerates (retards) to rest with a retardation of 3m/s2.
Step 2: Setting Up the Equations
Let:
- t1 = time taken to reach maximum velocity
- t2 = time taken to come to rest
From the problem, we know that the total time taken is:
t1+t2=10s
Step 3: Finding Time for Each Phase
Using the equations of motion, we can express t1 and t2 in terms of vmax:
1. For the acceleration phase:
vmax=u+at1
Here, u=0 (initial velocity), a=2m/s2, thus:
vmax=0+2t1⟹t1=vmax2
2. For the retardation phase:
0=vmax−3t2
Rearranging gives:
3t2=vmax⟹t2=vmax3
Step 4: Substitute into Total Time Equation
Now substitute t1 and t2 into the total time equation:
vmax2+vmax3=10
Step 5: Finding a Common Denominator
The common denominator for 2 and 3 is 6. Thus, we can rewrite the equation:
3vmax6+2vmax6=10
Combining the fractions gives:
5vmax6=10
Step 6: Solve for vmax
Now, multiply both sides by 6:
5vmax=60
Dividing by 5:
vmax=12m/s
Conclusion
The maximum speed attained by the body is:
12m/s
The body has two phases of motion:
1. Acceleration Phase: The body accelerates from rest with an acceleration of 2m/s2 until it reaches its maximum velocity vmax.
2. Retardation Phase: The body then decelerates (retards) to rest with a retardation of 3m/s2.
Let:
- t1 = time taken to reach maximum velocity
- t2 = time taken to come to rest
t1+t2=10s
Using the equations of motion, we can express t1 and t2 in terms of vmax:
vmax=u+at1
Here, u=0 (initial velocity), a=2m/s2, thus:
vmax=0+2t1⟹t1=vmax2
0=vmax−3t2
Rearranging gives:
3t2=vmax⟹t2=vmax3
Now substitute t1 and t2 into the total time equation:
vmax2+vmax3=10
The common denominator for 2 and 3 is 6. Thus, we can rewrite the equation:
3vmax6+2vmax6=10
Combining the fractions gives:
5vmax6=10
Now, multiply both sides by 6:
5vmax=60
Dividing by 5:
vmax=12m/s
The maximum speed attained by the body is:
12m/s
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - D)
24 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
A body starting from rest has an acceleration of 5m/s2. Calculate the distance travelled by it in 4th second.
View SolutionA train starte from rest and moves with a constant acceleration of 2ms−2 for half a minute. The brakes are then applied and the train comes to rest in one minute.find (i) the maximum speed attained by the train (ii) the total distance moves by the train and (ii) the positions (s) of the train a half the maximum speed.
View Solution
Knowledge Check
If a trolley starts from rest with an accerelaton of 2ms2, the velocity of the body after 4 s would be
A2m/sB8m/sC4m/sD6m/sA body starts from 20 m/s. If its acceleration is 2m/s2, then velocity of the body after 10 seconds is,-
A40 m/s,B20 m/s,C30 m/s,D10 m/sA body moves from rest with a constant acceleration of 5m/s2. Its instantaneous speed (in m/s) at the end of 10 sec is
A50B5C2D0.5
A body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionBetween two stations a train starting from rest first accelerates uniformly, then moves with constant velocity and finally retarts uniformly to come to rest. If the ratio of the time taken be 1:8:1 and the maximum speed attained be 60km/h, then what is the average speed over the whole journey ?
View SolutionA body starts from rest at time t=0 , the acceleration time graph is shown in the figure . The maximum velocity attained by the body will be
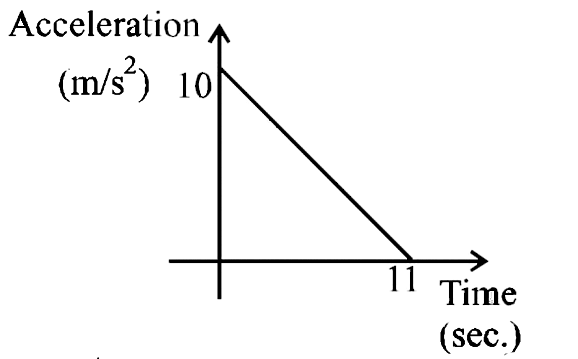
View SolutionA train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the speed of the train when the passenger catches it for the critical distance:
View Solution
