If the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
2 sec
2+√2sec
2−√2sec
zero
The correct Answer is:1
To find the time at which the acceleration of the particle is zero, we need to follow these steps:
Step 1: Write down the given velocity function.
The velocity v of the particle is given by:
v=3t2−12t+6
Step 2: Determine the acceleration function.
Acceleration a is the derivative of velocity with respect to time t. Therefore, we differentiate the velocity function:
a=dvdt=ddt(3t2−12t+6)
Using the power rule of differentiation:
a=6t−12
Step 3: Set the acceleration equal to zero.
To find when the acceleration is zero, we set the acceleration function to zero:
6t−12=0
Step 4: Solve for t.
Now, we solve for t:
6t=12
t=126=2
Conclusion:
The acceleration of the particle is zero at t=2 seconds.
The velocity v of the particle is given by:
v=3t2−12t+6
Acceleration a is the derivative of velocity with respect to time t. Therefore, we differentiate the velocity function:
a=dvdt=ddt(3t2−12t+6)
Using the power rule of differentiation:
a=6t−12
To find when the acceleration is zero, we set the acceleration function to zero:
6t−12=0
Now, we solve for t:
6t=12
t=126=2
The acceleration of the particle is zero at t=2 seconds.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
The position of a particle moving in x-y plane changes with time t given by →x=3t2ˆi+9tˆj. The acceleration of particle would be
A2 m/s^2B3 m/s^2C4 m/s^2D6 m/s^2If velocity of a particle is given by v=2t2−2 then find the acceleration of particle at t = 2 s.
A0B2C4D8vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
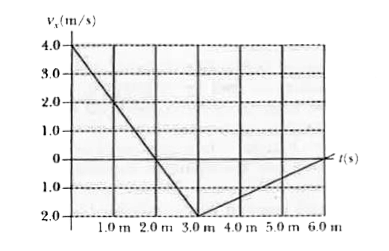 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
The velocity of a particle is given by v=12+3(t+7t2). What is the acceleration of the particle?
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View Solution
