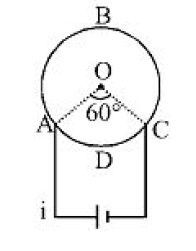
A cell is connected between the points A and C of a circular conductor ABCD of centre . If are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio , is
6
1
5
The correct Answer is:C
Now , [ as ]
Similar Questions
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
View Solution
Knowledge Check
A cell is connected between the points A and Cofa circular conductor ABCDA of centre O. ∠AOC=60∘. If B1, and B2, are the magnitudes of the magnetic fields at O due to currents in ABC and ADC respectively, the ratio B1/B2, is
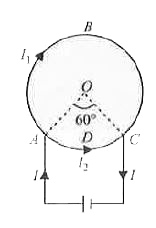 A6B5C1D1/5
A6B5C1D1/5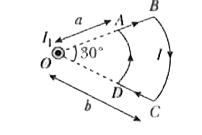
The magnitude of the magnetic filed B due to the loop ABCD at origin (O) isAzeroBμ0I(b−a)24πabCμ0I(b−a)4πabDμ0I4π[2(b−a)+π3(a+b)].The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is
 AzeroBμ0(b−a)24abCμ0I4π[b−aab]Dμ0I4π[2(b−a)+π3(a+b)]
AzeroBμ0(b−a)24abCμ0I4π[b−aab]Dμ0I4π[2(b−a)+π3(a+b)]
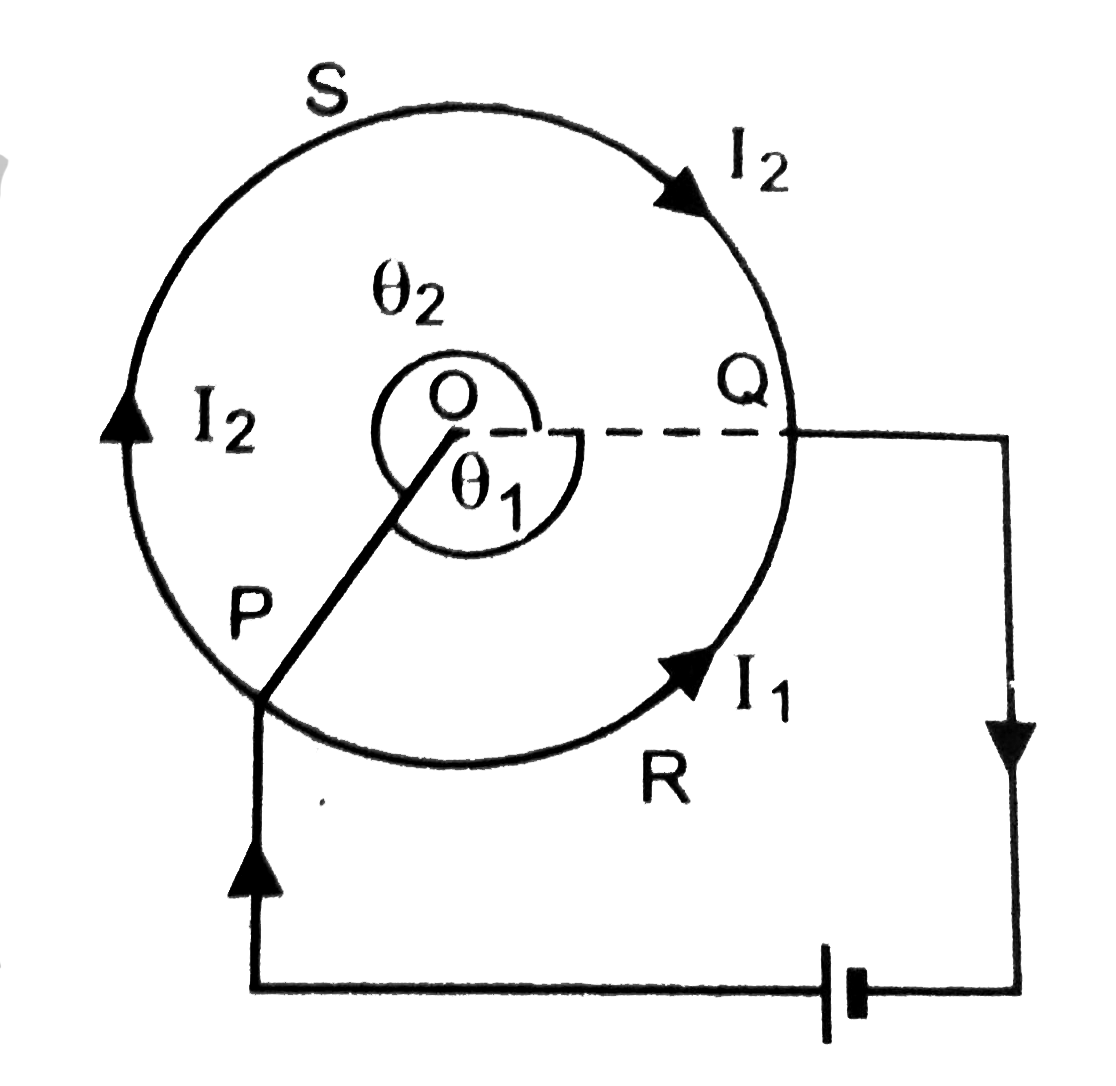
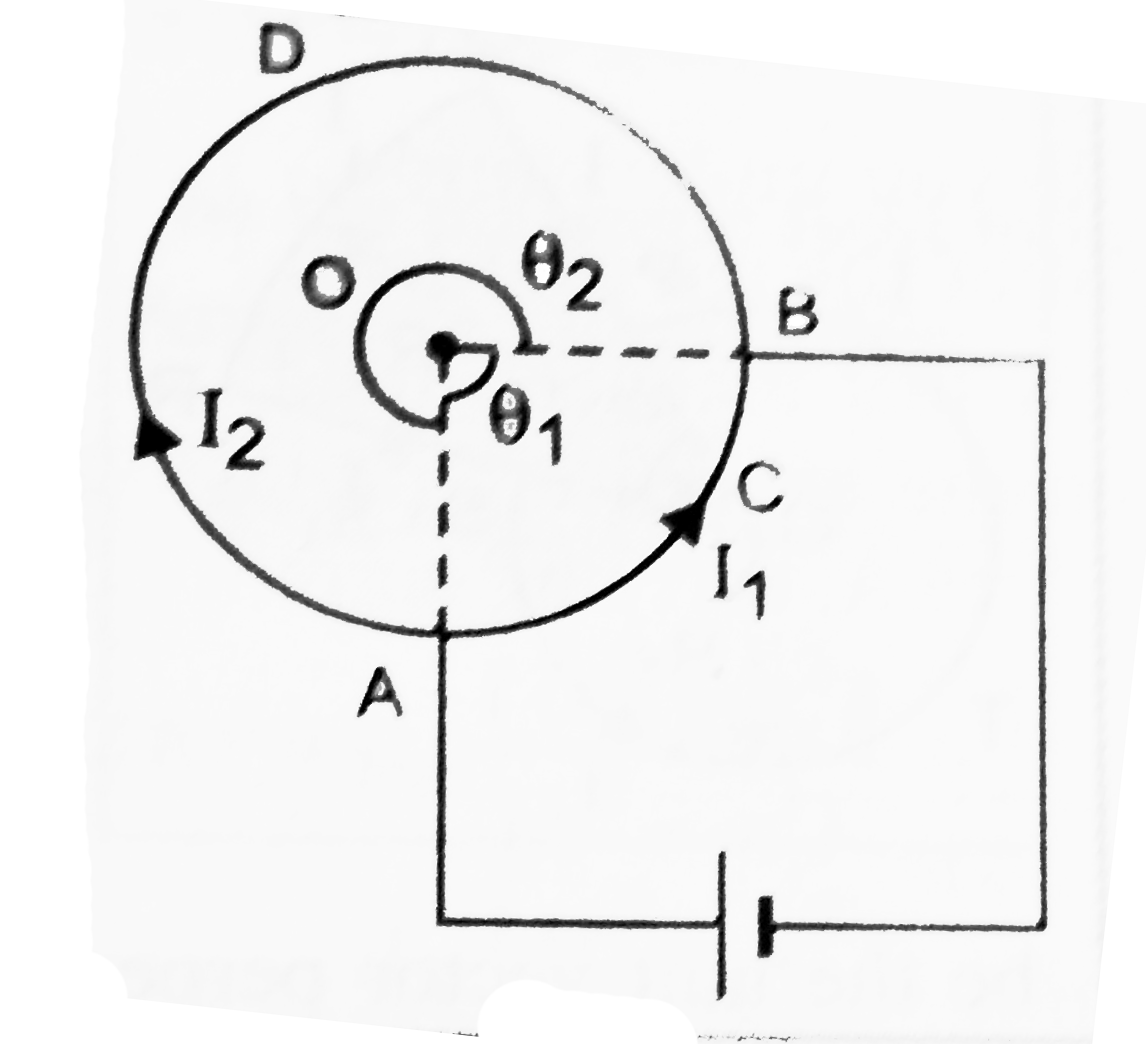
A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
View SolutionThe figure shows tow coaxial circulalr loop a1 and 2, which forms same solid angle θ at point O. If B1 and B2 are the magnetic fields produced at the point O due to loop 1 and 2 respectively, then

View SolutionA magnetic compass needl oscillates 30 times per minute at a place where the dip is 45∘ and 40 times per minute where the dip is 30∘ if B1 and B2 are respectively the total magnetic field due to the earth at the two places then the ratio B1/B2 is best given by
View SolutionIf the angles of a triangle ABC are in the ratio 2:3:1 then the angles A,B and C are
View SolutionA and B are two concentric circular conductors of centre O and carrying currents i1 and i2 as shown in the adjacent figure. If ratio of their radii is 1:2 and ratio of the flux densities at O due to A and B is 1:3, then the value of i1/i2 is

View Solution