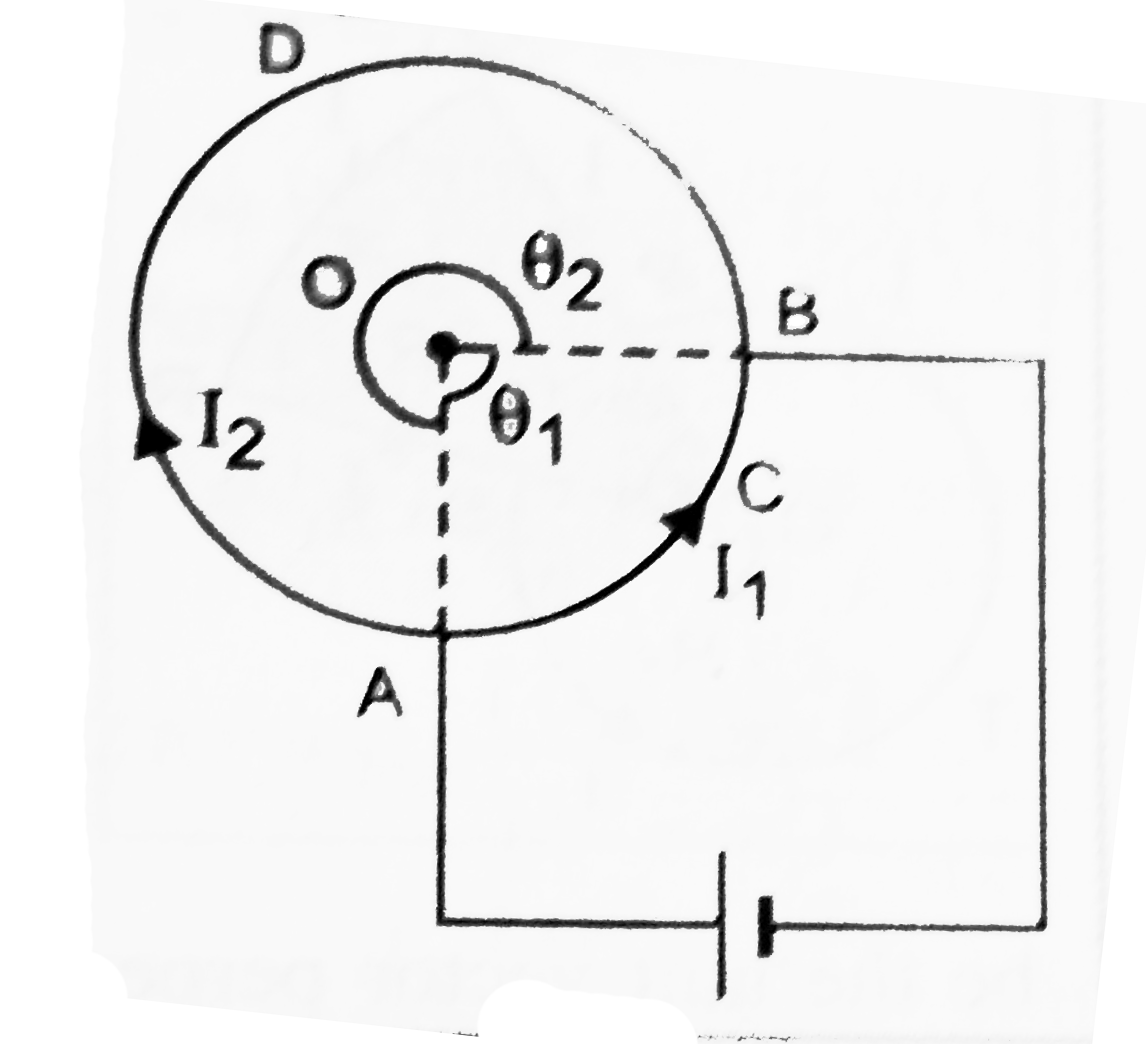
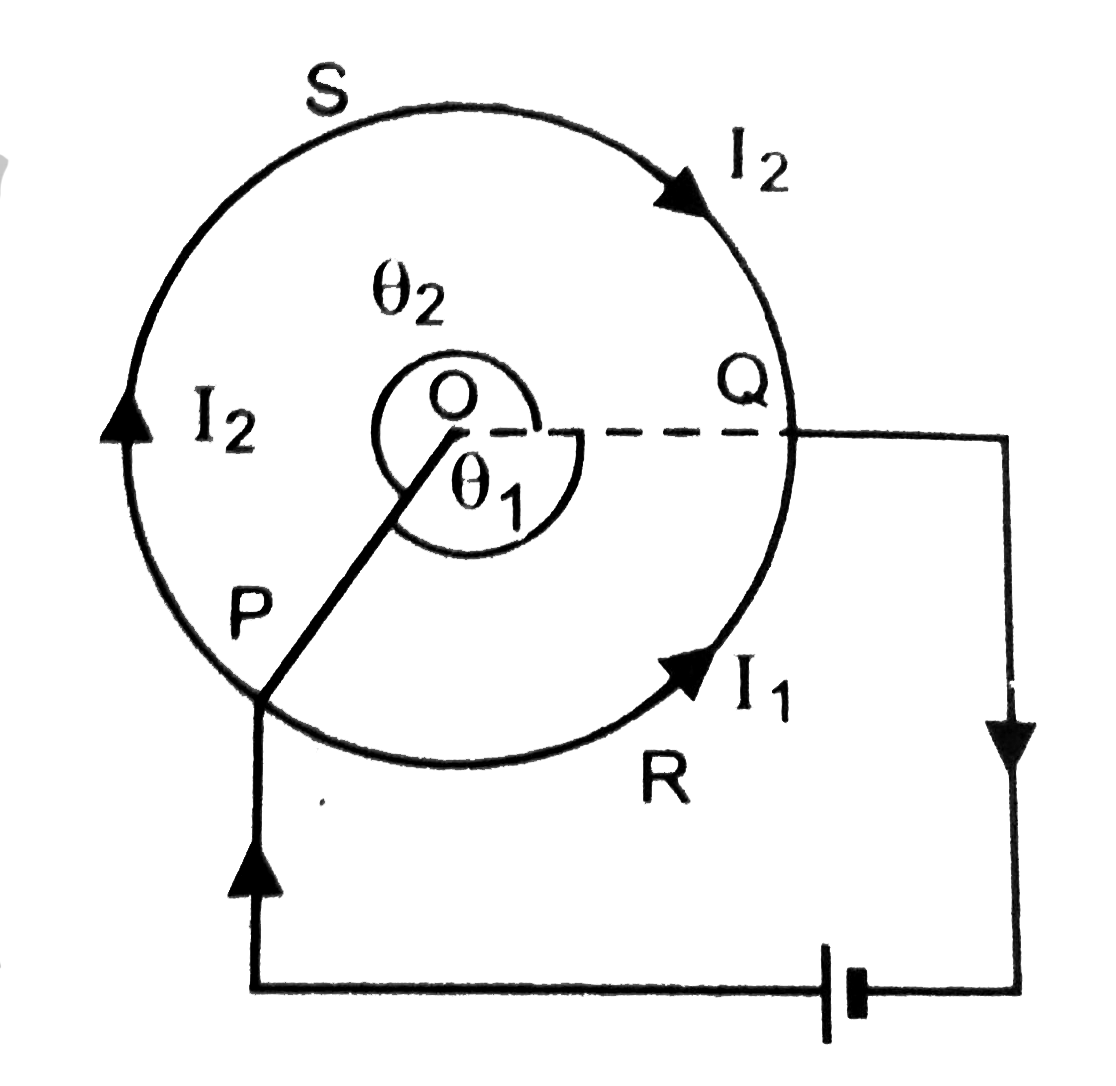
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
Video Solution
Text Solution
Let I1, I2 be the length of the two parts PRQ and PSQ of the circular conductor and ρ be the resistance per unit length of this conductor. Let r be the radius of circular conductor.
Resistance of the portion PRQ will be
R1=ρl1=ρrθ1
Resistance of the portion PSQ will be
R2=ρl2=ρrθ2
Let I1 and I2 be the currents in the portion PRQ and PSQ respectively.
The potential difference across P and Q is
VP−VQ=I1R1=I2R2
or I1ρrθ1=I2ρrθ2 or I1θ1=I2θ2 ...(i)
According to Biot Savart's law, the magnetic field induction at the centre O due to current through portions PRQ and PSQ will be
B1=μ04πI1θ1r and B2=μ04πI2θ2r
According to Right Hand Rule, the direction of →B1 and →B2 are opposite to each other, along a straight line. Hence the resultant magnetic field at O is
B=B1−B2 acting upwards =μ04πI1θ1r−μ04pI2θ2r=0(∵I1θ1=I2θ2)
Hence, the resultant magnetic field at O will be zero.
|
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
Knowledge Check
A cell is connected between two points of a uniformly thick circular conductor. The magnetic field at the centre of the loop will be
(Here i1 and i2 are the currents flowing in the two parts of the circular conductor of radius 'a' and μ0 has the usual meaning)AZeroBμ02a(i1−i2)Cμ02a(i1+i2)Dμ0a(i1+i2)In the figure, what is the magnetic field at the point O?
 Aμ0I4πrBμ0I4πr+μ0I2πrCμ0I4r+μ0I4πrDμ0I4r−μ0I4πr
Aμ0I4πrBμ0I4πr+μ0I2πrCμ0I4r+μ0I4πrDμ0I4r−μ0I4πrIn the figure shown, the magnetic field at the point O is
 Aμ04Ir(π+l)Bμ04Ir(π+2)Cμ04Ir(π−2)Dμ04Ir
Aμ04Ir(π+l)Bμ04Ir(π+2)Cμ04Ir(π−2)Dμ04Ir
Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
View SolutionFind the magnetic field at point O shown in the figure

View SolutionIn figure what is the magnetic field induction at point ‘O’?

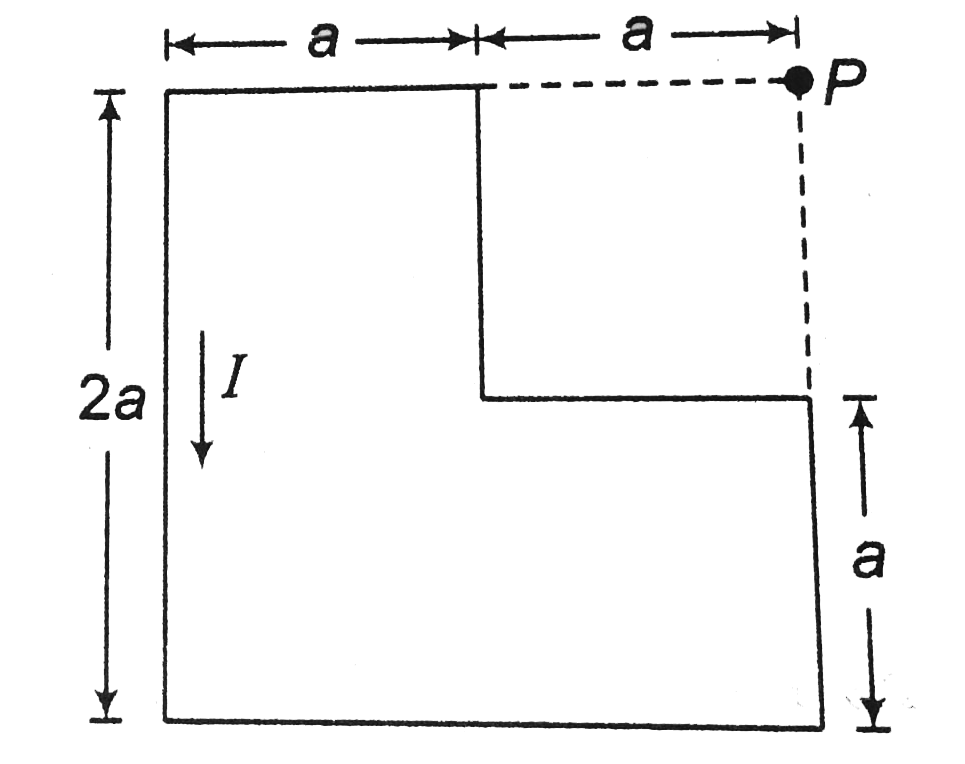
View SolutionFind the magnetic field B at the point P in figure
View SolutionOn connecting a battery to the two corners of a diagonal of a square conductor frame of side a the magnitude of the magnetic field at the centre will be
View Solution