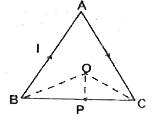
An equilateral triangle is made by uniform wires AB, BC, CA. A current I enters at A and leaves from the mid point of BC. If the lengths of each side of the triangle is L, the magnetic field B at the centroid O of the triangle is
μ04π(4IL)
μ02π(4IL)
μ04π(2IL)
Zero
The correct Answer is:D
Magnetic field due to AB and BD is outside to the plane = B1
Magnetic field due to AC and CD is inside to plane = B2
∴→B1+→B2=0
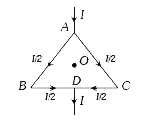
Similar Questions
Knowledge Check
A current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
A1.66×10−6TB1.22×10−4TC1.33×10−6TD1.44×10−4TA conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
A2√3μ0I4πLBμ0I4πLC√3μ0I4πLDzeroThe current I ampere is flowing in an equilateral triangle of side a the magnetic field induction at the centroid will be
A9μ0I2πaB5√2μ0I3πaC3μ0I2πaDμ0I3√3πa
An equilateral triangle of side 10cm carries a current of 3A. Find the magnetic field at centroid of triangle.
View SolutionThe wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.

View SolutionABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View SolutionA current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png)
View Solution