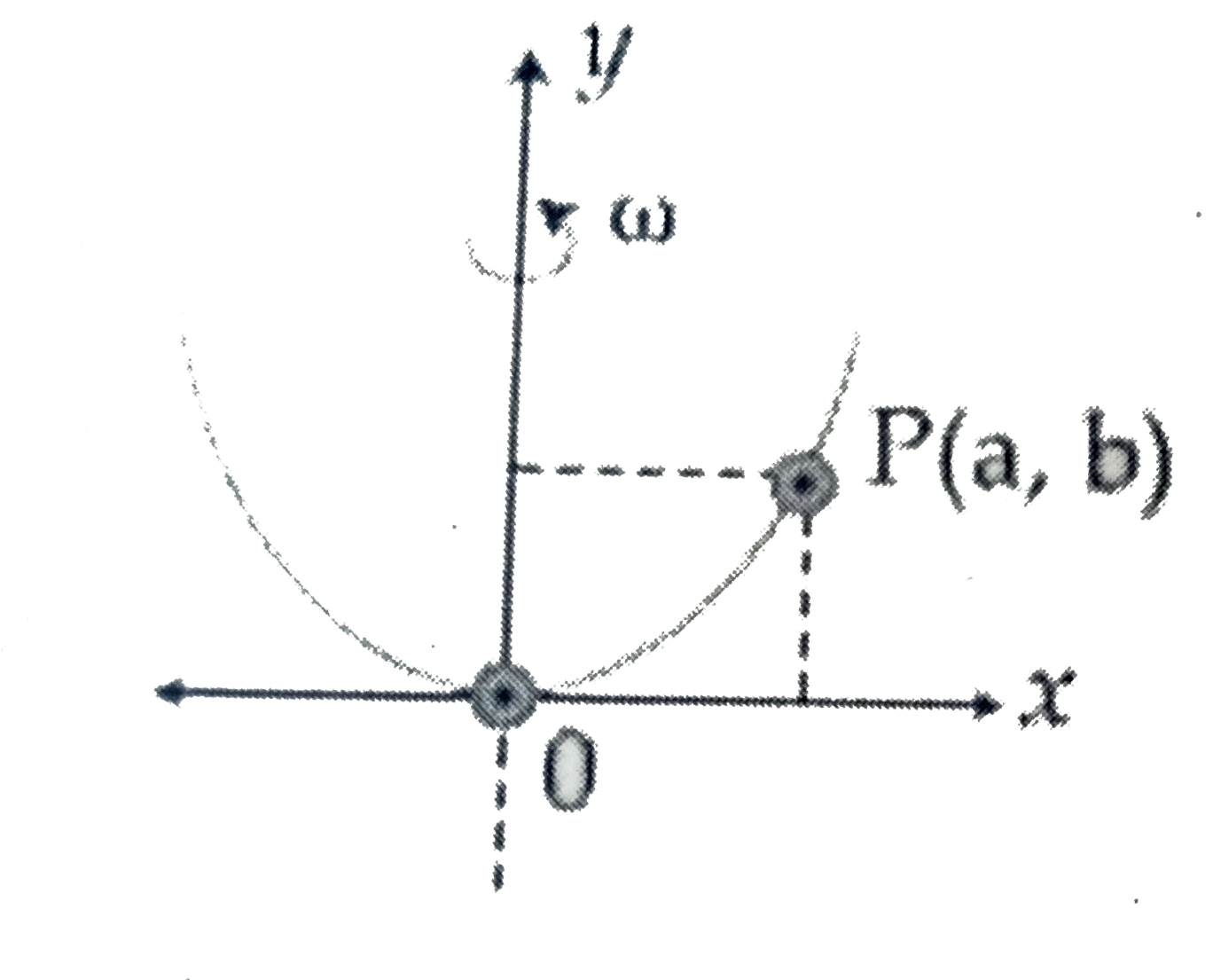
A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
2√2gC
2√gC
√2gCab
√2gC
The correct Answer is:A

y=4Cx2
dydx=tanθ=8Cx
At P tanθ=8Cx
For steady circular motion -
mgsinθ=mω2xcosθ
implies tanθ=ω2xg⇒8Cx⋅g=ω2⋅x
implies ω=√8gC⇒ω2√2gC
Similar Questions
A piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y =4 Cx^(2) and rotating with angular speed omega (see figure ) . The value of omega is (neglect friction),
View SolutionA piece of wire is bent in the shape of a parabola y = kx^2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA wire which is bent in the shape of a curve given by, y=a3x4. A bead of mass m is located at point P(x,y). If the wire is smooth, find ω with which wire needs to be rotated for bead to be static.
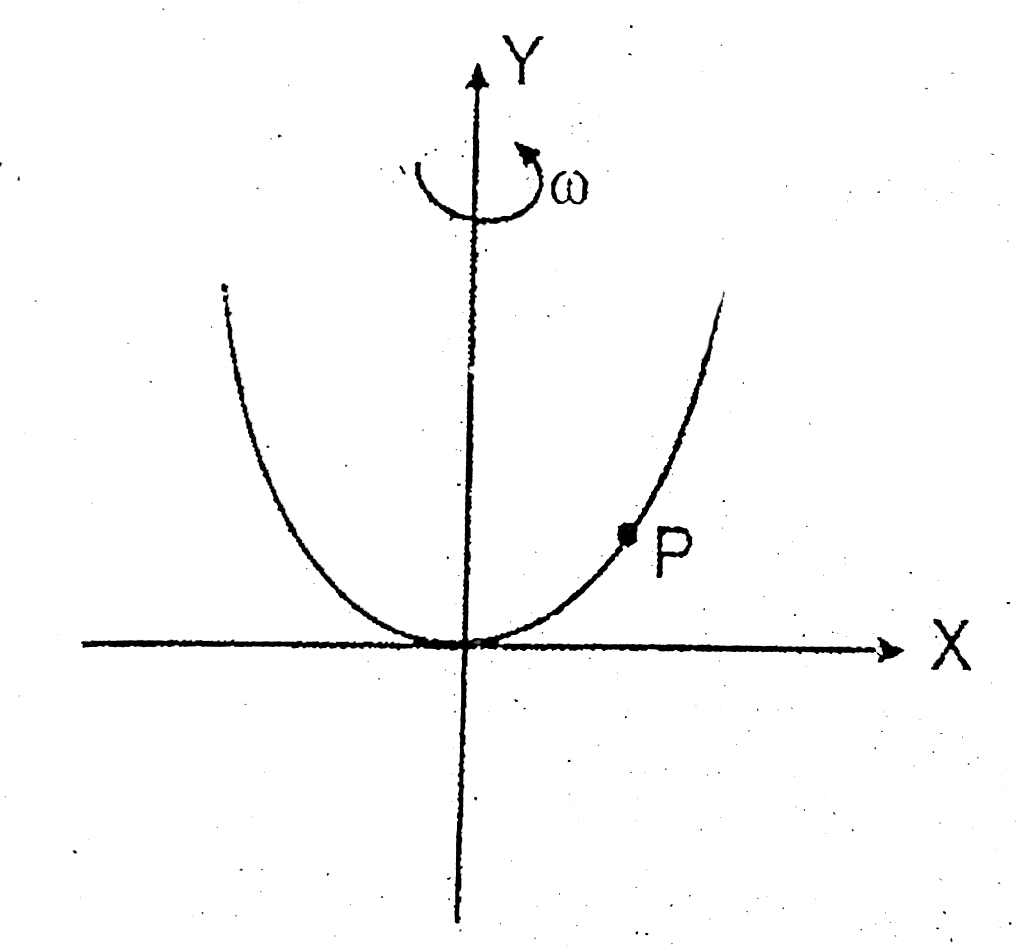
View SolutionA smooth wire frasme is in the shape of a parabola y=5x2 . It is being rotated about y-axis with an angular velocity ω. A small bead of mass (m=1kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity ω is (g=10m/s2)
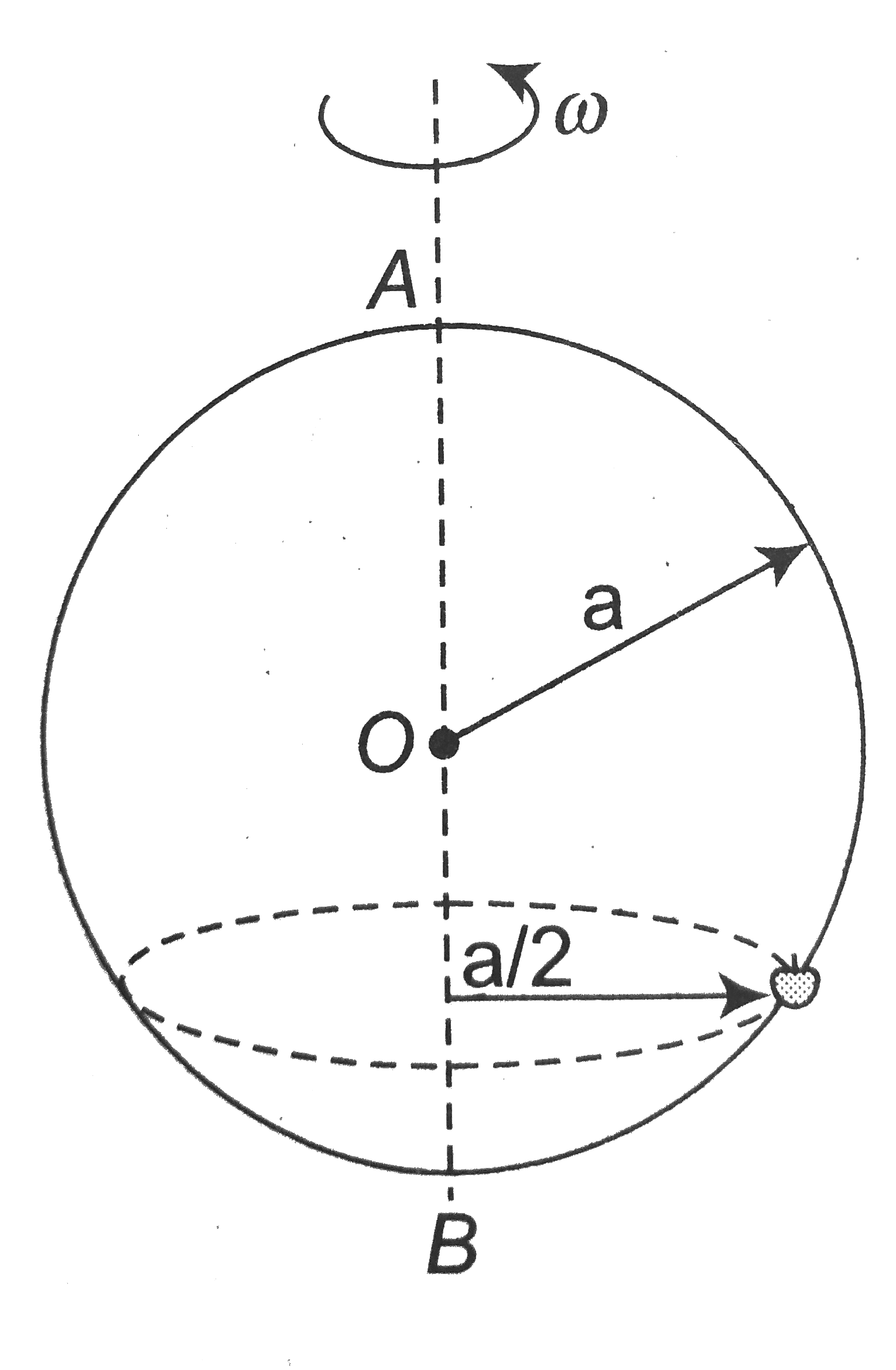
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solution
