A smooth wire frasme is in the shape of a parabola $y = 5 x^{2}$ . It is being rotated about y-axis with an angular velocity $ω$ . A small bead of mass $(m = 1 k g)$ is at point $P$ and is in equilibrium with respect to the frame. Then the angular velocity $ω$ is $(g = 10 m / s^{2})$

A

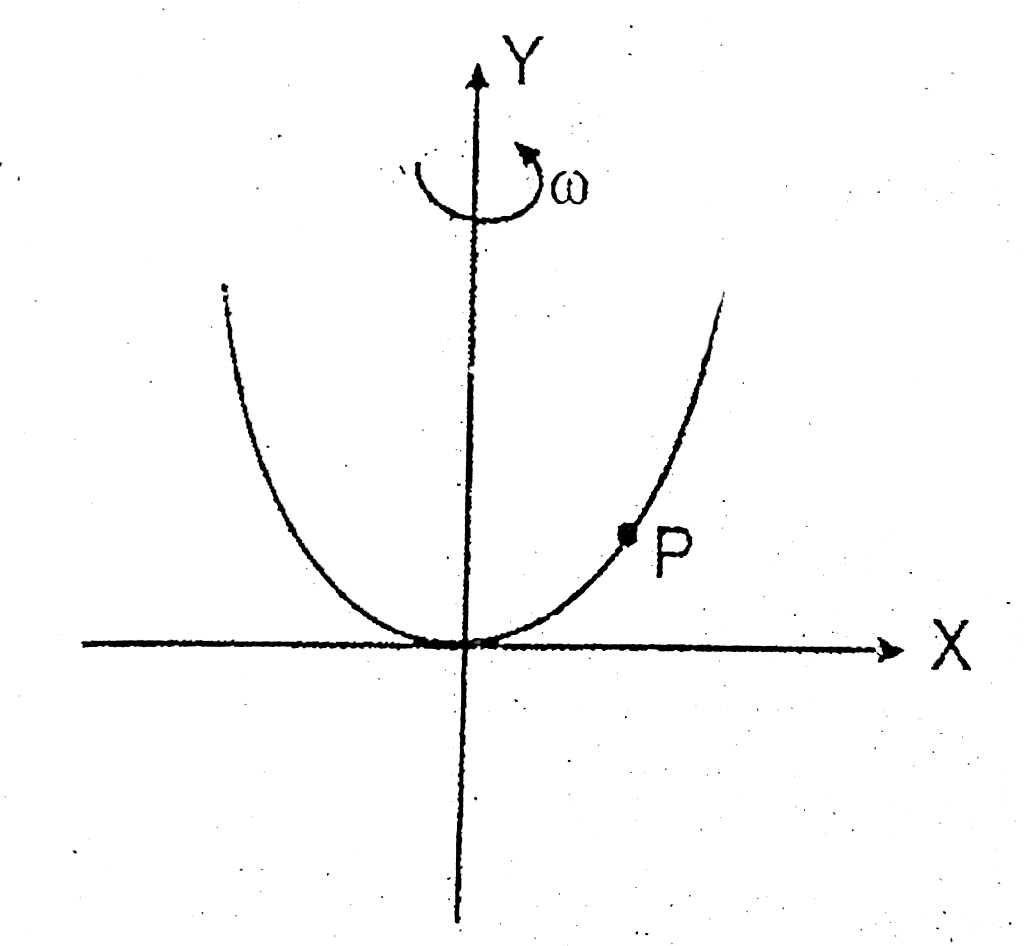
$ω = 5 r a d / sec$

B

$ω = 10 r a d / sec$

C

$ω = 20 r a d / sec$

D

Depends of x-coordinate of particle

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

A smooth wire …………

$(1) m ω^{2} x cos θ = m g sin θ \Rightarrow tan θ = \frac{ω^{2} x}{g}$
$tan θ = \frac{d y}{d x} = 10 x$
$ω = 10 r a d / sec$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
A thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity $ω$ . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
A $\frac{ω M}{(m + M)}$
B $\frac{ω (M - 2 M)}{(M + 2 m)}$
C $\frac{ω M}{(M + 2 m)}$
D $\frac{ω (M + 2 m)}{M}$
Question 2 - Select One
A thin circular ring of mass $m$ and radius $R$ is rotating about its axis with a constant angular velocity $ω$ . Two objects each of mass $M$ are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity $ω' =$
A $\frac{ω (m + 2 M)}{m}$
B $\frac{ω (m - 2 M)}{(m + 2 M)}$
C $\frac{ω m}{(m + M)}$
D $\frac{ω m}{(m + 2 M)}$
Question 3 - Select One
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
A $\frac{M ω}{M + 4 m}$
B $\frac{(M + 4 m) ω}{M}$
C $\frac{(M - 4 m) ω}{M + 4 m}$
D $\frac{M ω}{4 m}$

Recommended Questions

Home
Ask Doubt
Profile