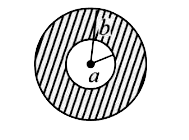
A circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc varies as (σ0r). then the radius of gyration of the disc about its axis passing through the centre is:
a+b2
√a2+b2+ab2
√a2+b2+ab3
a+b3
The correct Answer is:C
I=∫dm.r2
I=∫baσ0r2πrdr.r2
⇒I=σ02π(b3−a33)
M=∫badm=∫baσ0r2πrdr=σ02π(b−a)
I=MK2
σ02π(b3−a33)=σ02π(b−a)K2
=K=√a2+b2+ab3
Similar Questions
From a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionA circular disc of radius b has a hole of radius a at its centre (see figure) if the mass per unit area of the disc varies as ((sigma_(0))/(r)) then the radius of gyration of the disc about its axis passing through the centre is
View SolutionA disc of mass .m. and radius R has a concentric hole of radius .r.. Its M.I. about an axis through centre and normal to its plane is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of disc is 2m, the radius of gyration of disc about an axis passing through its diameter is
View SolutionRatio of radius of gyration of a thin uniform circular disc about the axis passing through its centre and normal to its plane to radius of gyration of the same disc about its diameter is
View SolutionRadius of gyration of the disc about a transverse axis passing through its centre is 14.14 cm. Then its radius of gyration about its diameter is
View Solution
