The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
2 m
2 cm
1 m
0.2 m
The correct Answer is:C
To find the radius of gyration of a disc about an axis passing through its diameter, we can follow these steps:
1. Identify the Given Data:
- The radius of the disc (r) = 2 m.
2. Understand the Concept of Radius of Gyration:
- The radius of gyration (k) is related to the moment of inertia (I) of the object. It is defined by the equation:
I=m⋅k2
where m is the mass of the disc.
3. Calculate the Moment of Inertia of the Disc:
- The moment of inertia of a disc about an axis passing through its diameter is given by:
I=14mr2
4. Set Up the Equation Using the Radius of Gyration:
- From the definition of the radius of gyration, we can equate the two expressions for moment of inertia:
14mr2=mk2
5. Cancel the Mass (m) from Both Sides:
- Since mass m appears on both sides of the equation, we can cancel it out:
14r2=k2
6. Solve for the Radius of Gyration (k):
- Taking the square root of both sides gives:
k=√14r2=r2
7. Substitute the Value of r:
- Now substitute the value of the radius r=2 m into the equation:
k=22=1 m
8. Conclusion:
- The radius of gyration of the disc about an axis passing through its diameter is:
k=1 m
Final Answer:
The radius of gyration of the disc is 1 meter.
---
- The radius of the disc (r) = 2 m.
- The radius of gyration (k) is related to the moment of inertia (I) of the object. It is defined by the equation:
I=m⋅k2
where m is the mass of the disc.
- The moment of inertia of a disc about an axis passing through its diameter is given by:
I=14mr2
- From the definition of the radius of gyration, we can equate the two expressions for moment of inertia:
14mr2=mk2
- Since mass m appears on both sides of the equation, we can cancel it out:
14r2=k2
- Taking the square root of both sides gives:
k=√14r2=r2
- Now substitute the value of the radius r=2 m into the equation:
k=22=1 m
- The radius of gyration of the disc about an axis passing through its diameter is:
k=1 m
The radius of gyration of the disc is 1 meter.
Topper's Solved these Questions
Similar Questions
Calculate the radius of gyration of a uniform circular ring about an axis passing through its diameter.
View SolutionThere is a uniform circular disc of mass 10kg & radius 2 meter. Calculate the radius of gyration if it is rotating about an axis passing through its centre & perpendicular to its plane
View Solution
Knowledge Check
Radius of gyration of a ring about a transverse axis passing through its centre is
A0.5× diameter of ringBdiameter of ringC2× diameter of ringD(diameter of ring)2The radius of gyration of a disc about an axis coinciding with a tangent in its plane is
AR2BR√2C√2RD√52RThe radius of gyration of a disc of mass 100 g and radius 5 cm about an axis passing through its centre of gravity and perpendicular to the plane is
A0.5 cmB2.5 cmC3.54 cmD6.54 cm
The radius of gyration of a disc of mass 50 g and radius 2.5 cm, about an axis passing through its centre of gravity and perpendicular to the plane is
View SolutionA circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc varies as (σ0r). then the radius of gyration of the disc about its axis passing through the centre is:
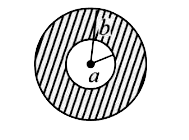
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is I. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View SolutionCalculate the radius of gyration of a circular disc about its diameter.
View SolutionThe radius of gyration of a thin disc of radius 4 cm about a diameter is
View Solution
