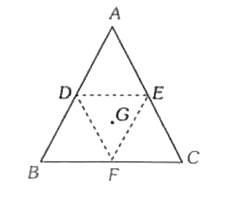
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I0 If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

I=916I0
I=1516I0
I=34I0
I=I04
The correct Answer is:B
From Dimension analysis I0=kMa2
Now for small lamina
I=kM4(a2)2=kMa216⇒I=I016
So moment of inertia of remaining part I−I=15I016
Similar Questions
एक पतले ठोस लकड़ी के फलक से एक त्रिभुज ABC काटा गया हैं (चित्र देखिए) दर्शाए गये अनुसार D, E तथा F इसकी भुजाओं के मध्य बिन्दु हैं तथा G त्रिभुज का केन्द्र है। G से गुजरने वाली तथा त्रिभुज के समतल के लम्बवत् अक्ष के सापेक्ष त्रिभुज का जडत्व आघूर्ण I0. है। यदि छोटा त्रिभुज DEF त्रिभुज ABC में से निकाल लिया जाये तो शेष बचे हुए भाग का उसी अक्ष के सापेक्ष जडत्व आघूर्ण है। तब
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionAn equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I_(0) If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :
View SolutionThree particles each of mass 100 g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid of the triangle and perpendicular to its plane.
View Solution
Three solids sphere each of mass m and diameter d are stuck together such that the lines connecting the centers from an equilateral triangle of side of length d. The ratio I0IA of moment of inertia I0 of the system about an axis passing the centroid and about center of any of the spheres IA and perpendicular to the plane of the triangle is
View SolutionD,E,F are the mid points of the sides BC, CA and AB respectively of a △ABC. Determine the ratio of the areas of △DEF and △ABC.
View SolutionIf D,E,F are mid-points of the sides of triangle ABC , prove (by vectors) that area of triangle DEF= 1/4 area of triangle ABC .
View SolutionThe mid-points of the sides of an equilateral triangle ABC are DE and F. triangle DEF and triangle The ratio of the areas of the DCF will be
View Solution

