A wheel of radius R with an axle of radius R/2 is shown in the figure and is free to rotate about a frictionless axis through its centre and perpendicular to the page. Three forces (F, F, 2F) are exerted tangentially to the repective rims as shown in the figure.
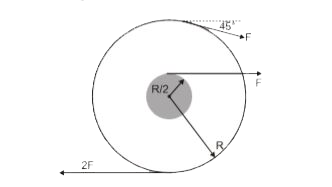
The magnitude of the net torque acting on the system is nearly
3.5 FR
3.2 FR
2.5 FR
1.5 FR
The correct Answer is:A
τNet=F(R2)+FR+2FR=3.5FR
Similar Questions
A uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
06:06View SolutionA wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
01:23View SolutionThree forces of magnitude F, F and sqrt(2F) are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
02:37View SolutionOn a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
03:00View SolutionOn a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
05:01View SolutionRadius of gyration of disc rotating about an axis perpendicular to its plane passing through its centre is (If R is the radius of disc)
01:43View SolutionFour spheres , each of mass M and radius r, are situated at the four corners of a square of side R, as shown in figure. The moment of inertia of the system about an axis perpendicular to the plane of square and passing through its centre will be
View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
01:51View Solution