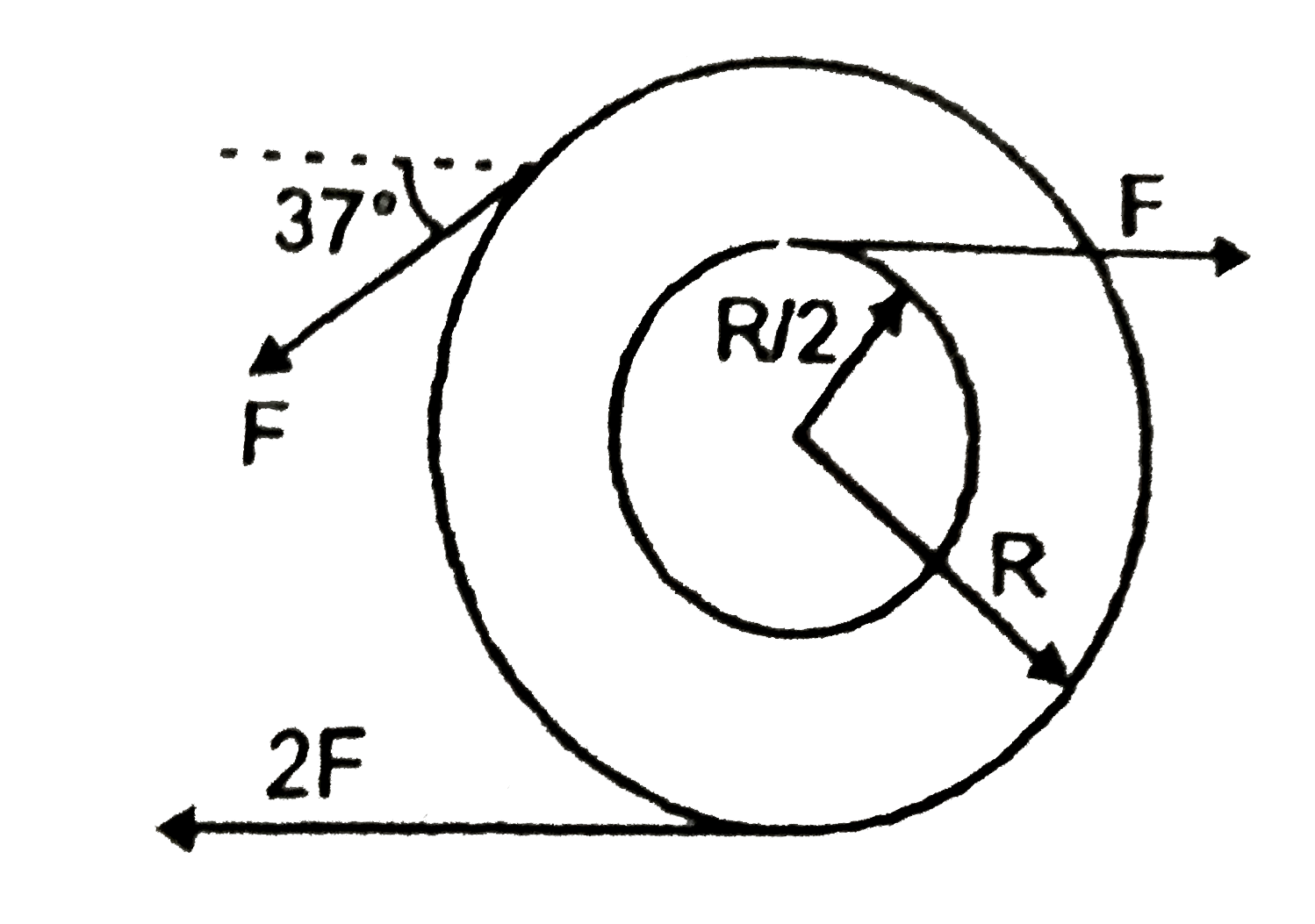
On a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
1.5FR
1.9FR
2.3FR
2.5FR
The correct Answer is:A
Torque τ=(2F)R+F(R2)+FR(−1)
=3FR2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp61
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 62
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.

View Solution