Two identical rods are joined at one of their ends by a pin. Joint is smooth and rods are free to rotate about the joint. Rods are released in vertical plane on a smooth surface as shown in the figure. The displacement of the joint from its initial position to the final position is (i.e. when the rods lie straight on the groun )
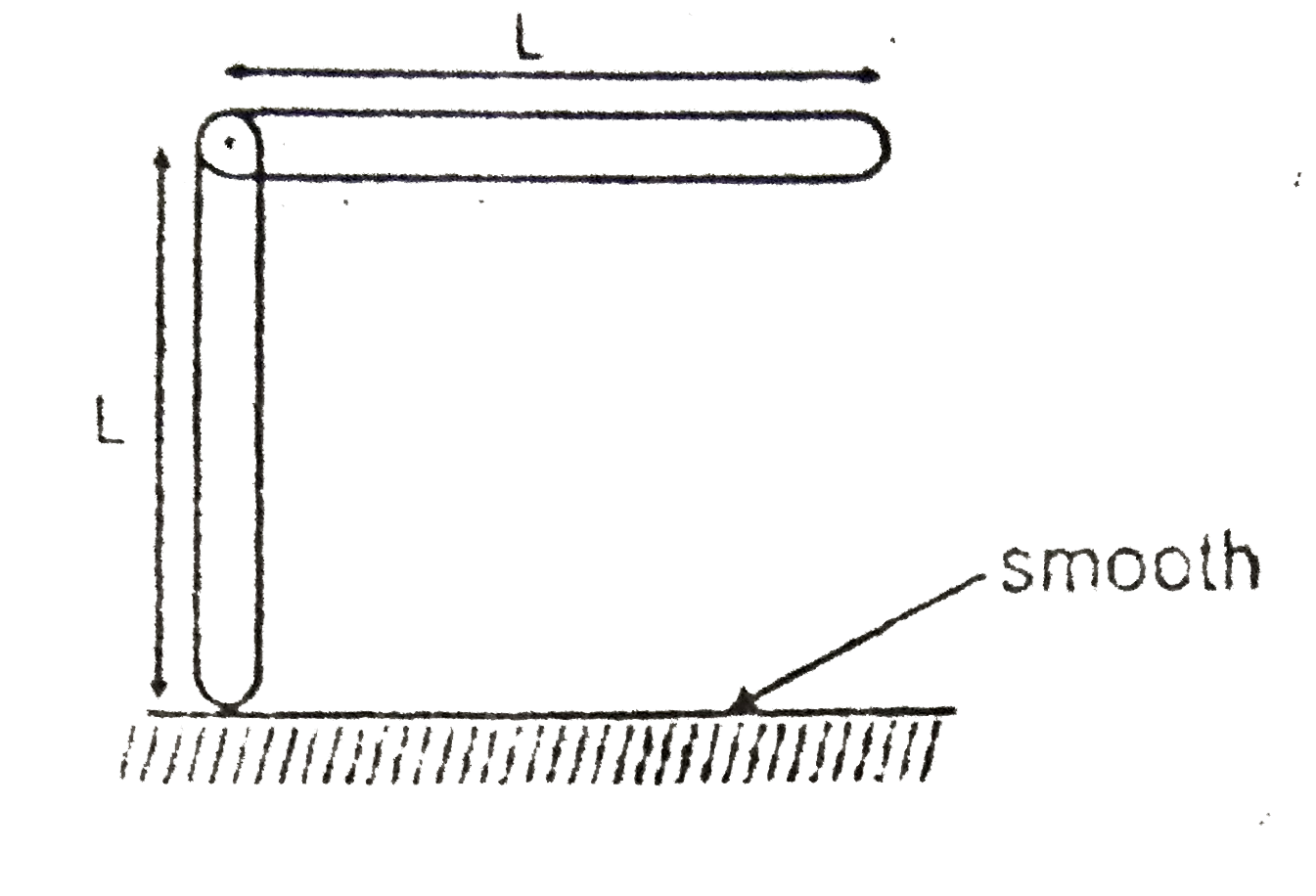
L4
√174
√15L2
none of these
The correct Answer is:B, D
Initailly the centre of mass is at L4 distance from the vertical rod.
⎛⎜
⎜⎝As,xcm=m(12)+m0m+m=L4⎞⎟
⎟⎠
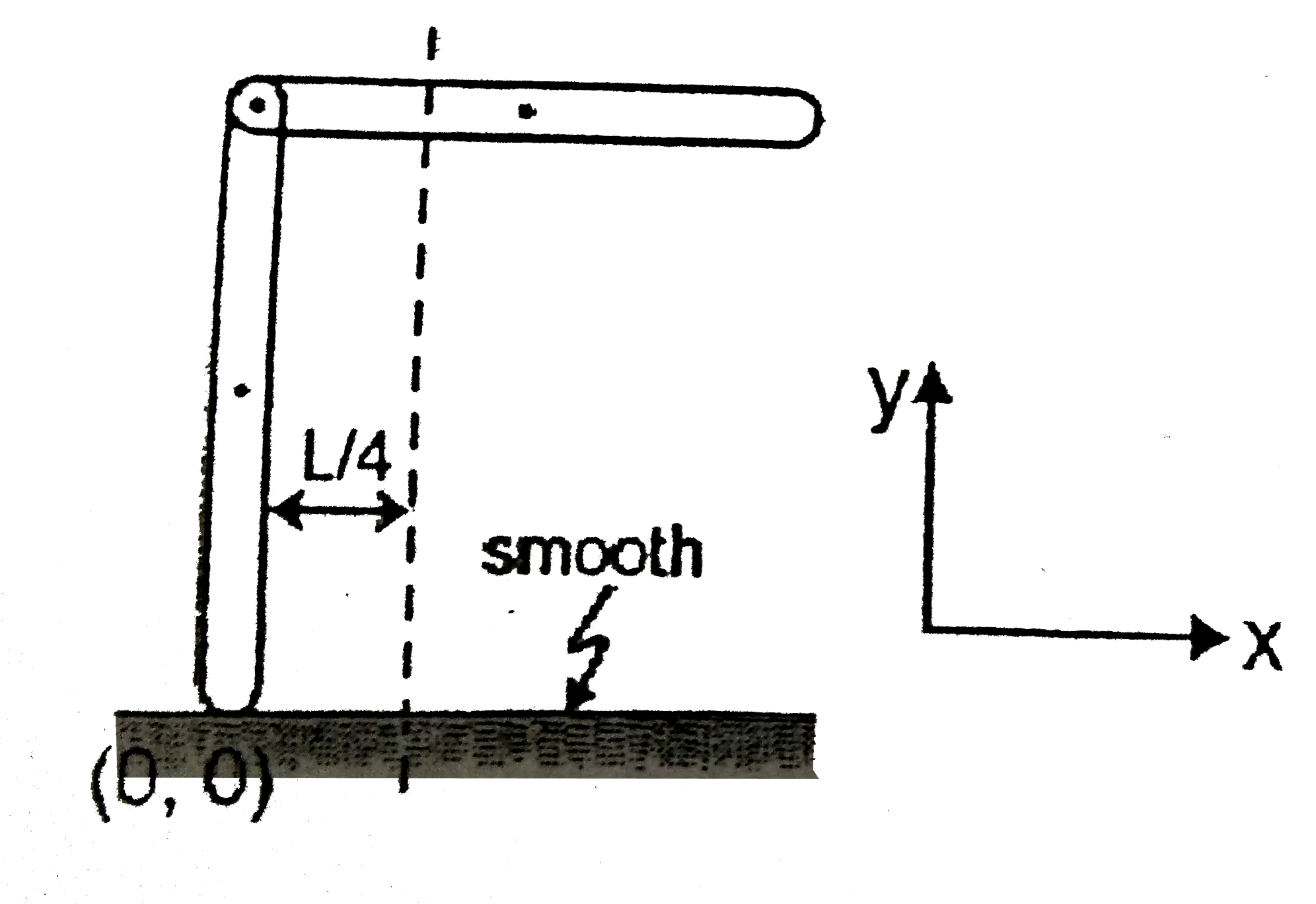
centre of mass does not move in x− direction as ΣFx=0.
After they lie on the floor, the pin joint should be at L/4 distance from the origin shown inorder to keep the centre of mass at rest.
∴Finally x− displacement of the pin is L4 and y− displacement of the pin is obviosuly L.
Hence net displacement =√L2−L216=√17L4
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp61
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 62
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionTwo equal rods joined at one end are kept on a smooth surface as shown and released Trajectory of centre of mass of both rods is :−

View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionA uniform rod is hinged at its one end and is allowed to rotate in verticle plANE. Rod is given angular velocity ω in its verticle position as shown in figure. The value of ω for the force exerted by the hinge on rod is zero in this position is

View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

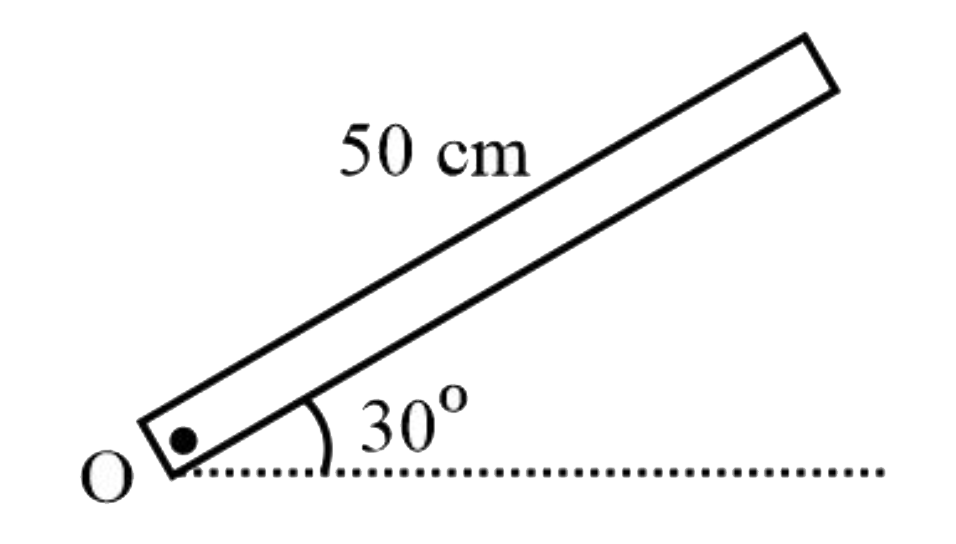
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View Solution
