A uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
E=2ε0σ(1(Z2+R2)1/2+Z)
E=σ2ε0(1+Z(Z2+R2)1/2)
E=σ2ε0(1−Z(Z2+R2)1/2)
E=σ2ε0(1(Z2+R2)+1Z2)
The correct Answer is:C
The disc can be considered to be a collection of large number of concentric rings. Consider an element of the shape of rings of radius r and of width dr. Electric field due to this ring at P is
dE=K.σ2πr.dr.x(r2+x2)3/2
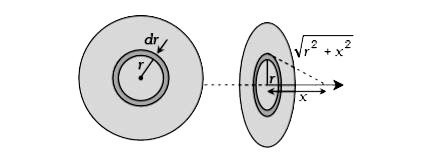
Put, r2+x2=y2
2rdr=2ydy
∴dE=K.σ2πy.dy.xy3=2Kσπ.xydyy3
Electric field at P due to all rings is along the axis,
∴E=∫dE
=2Kσπx√R2+x2∫x1y2dy=2Kσπx.[−1y]√R2+x2x
=2Kσπx[+1x−1√R2+x2]=2Kσπ[1−x√R2−x2]
=σ2ε0[1−x√R2+x2] along the axis.
Similar Questions
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View SolutionA charged disc of radius 3 m has charge density σ. Electric field at a distance of 4 m from its centre on axis is _______
View SolutionThe surface charge density of a thin charged disc of radius R is sigma . The value of the electric field at the centre of the disc (sigma)/(2 epsilon_0) . With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density sigma (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionFind the electric field potential and strength at the center of a hemisphere of radius R charged uniformly with the the surface density σ.
View SolutionA uniformly charged non conducting disc with surface charge density 10nC//m^(2) having radius R=3 cm . Then find the value of electric field intensity at a point on the perpendicular bisector at a distance of r=2cm
View SolutionThe surface charge density of a thin charged disc of radius R is sigma . The value of the electric field at the centre of the disc is (sigma)/(2epsi_0) . With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc
View SolutionA disc is kept on xy plane with centre at origin. Find electric field at a point with distance Z from origin on z-axis.
View Solution