In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :

A

$A \sqrt{\frac{M + m}{M}}$

B

$A \sqrt{\frac{M - m}{M}}$

C

$A \sqrt{\frac{M}{M + m}}$

D

$A \sqrt{\frac{M}{M - m}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

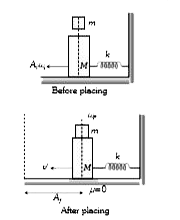
We know that $ω \sqrt{\frac{k}{M - m}} and ω_{1} = \sqrt{\frac{k}{M}} (A_{i} = A)$
Also, momentum is conserved just befor and just after the block of mass (m) is placed because there is no impulsive force . So,
$M A_{i} ω_{i} = (M + m) v .$
$v . = \frac{M A_{f} ω_{f}}{(M + m)}, v . = A_{f} ω_{f}$
$\frac{M A ω_{i}}{(M + m)} = A_{f} \sqrt{\frac{k}{(M + m)}}$
$\Rightarrow \frac{M a \sqrt{\frac{k}{M}}}{M + m} \times \sqrt{\frac{M + m}{k}} = A_{f}$
$\Rightarrow A_{f} = A \sqrt{\frac{M}{(M + m)}}$
Aliter : On putting m on M. Let velocity becomes B $(m + M) V = M V_{0}$ (by momentum conservation)
Now, kinetic Energy $= \frac{1}{2} (m + M) V^{2}$
$K . = \frac{1}{2} (m + M) \frac{M^{2} V_{0}^{2}}{{(m + M)}^{2}}$
$K . = \frac{1}{2} \frac{M^{2} V_{0}^{2}}{(M + m)}$ [ $∴ \frac{1}{2} M V_{0}^{2} = \frac{1}{2} k A^{2} and K . = \frac{1}{2} k {(A .)}^{2}$ ]
Hence $A . = \sqrt{\frac{M}{(M + m)}} A$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile