A person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.
The correct Answer is:107.4
The platform vibrates between the positions A and B about the mean position Q as shown in
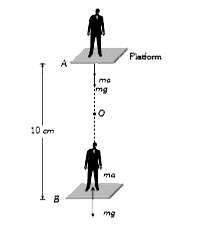
Given A = 5 . 0 cm
m=60kg,v=2Hz
At A and B the acceleration is maximum and is directed towards the mean position .
It is given by
amax=ω2A
=4π2v2A
=4×9.87×(2)2×0.05=7.9ms−2
At A, both the weight mg and the restoring force F and directed towards O .Therefore , the weight at A is maximum and is given by
W1=(mg+F)=(mg+mamax)=m(g+amax)
=60(10+7.9)=60×17.9=1074N
=1074g=107410=107.4kgf
Similar Questions
A boy is standing on a weighing machine placed on a horizontal platform. The reading of weighing machine is 70 kg. Using a suitable mechanism the platform is made to execute harmonic vibrations with a frequency of 1 vibration per second. Calculate the maximum and minimum force exerted on the boy if the amplitude of vibration of platform is 6 cm.
View SolutionA person is standing on the platform of a spring. Spring balance reading 60 Kg is weight. If the person jumps out of the platform, the Libra reading
View SolutionA person normally weighing 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0cm. A weighing machine on the platform gives the persons weight against time.
Will there be any change in weight of the body, during the oscillation?
View SolutionA person normally weighing 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s^(-1) and an amplitude 5.0 cm . A weighing machine on the platform gives the persons weight against time. If answer of part (1) is yes, what will be the maximum and minimum reading in the machine and at which position?
View SolutionA person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s^(-1) and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time. (a) Will there be any change in weight of the body, during the oscillation? (b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
View Solution50 kg भार का एक व्यक्ति एक ऐसे द्रव्यमान रहित प्लेटफार्म पर खड़ा है जो ऊपर-नीचे 2.0S−1 आवृति तथा 5.0 cm आयाम के आवर्ती दोलन कर प्लेटफार्म पर रखी एक तौल मशीन उस व्यक्ति का समय के बनाती है।
(a) क्या दोलन के दौरान व्यक्ति के भार में कोई परिवर्तन होगा?
(b) यदि भाग (a) का उत्तर हाँ है तो मशीन में उसके भार के भार क्या होंगे और ये मान किन स्थितियों पर अधिकतम और न्यूनतम होंगे ?
View SolutionPassage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec−1 and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (π2) = 10 and g = 10 m/s2. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
Which of the following will be correct for reading of weighting machine
View SolutionA person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.
View Solution
