A boy is standing on a weighing machine placed on a horizontal platform. The reading of weighing machine is 70 kg. Using a suitable mechanism the platform is made to execute harmonic vibrations with a frequency of 1 vibration per second. Calculate the maximum and minimum force exerted on the boy if the amplitude of vibration of platform is 6 cm.
To solve the problem, we need to calculate the maximum and minimum force exerted on the boy standing on a weighing machine that is vibrating harmonically. Here are the steps to arrive at the solution:
Step 1: Understand the Given Data
- The mass of the boy (m) = 70 kg
- The frequency of vibration (f) = 1 vibration per second
- The amplitude of vibration (A) = 6 cm = 0.06 m
- Acceleration due to gravity (g) = 10 m/s² (for simplicity)
Step 2: Calculate the Angular Frequency (ω)
The angular frequency (ω) is related to the frequency (f) by the formula:
ω=2πf
Substituting the value of f:
ω=2π×1=2π rad/s
Step 3: Calculate the Maximum Acceleration (a_max)
The maximum acceleration in harmonic motion can be calculated using the formula:
amax=Aω2
Substituting the values:
amax=0.06×(2π)2
Calculating (2π)2:
(2π)2≈39.478
Thus,
amax=0.06×39.478≈2.36868 m/s2
Step 4: Calculate the Maximum Force (F_max)
The maximum force exerted on the boy when the platform accelerates upwards can be calculated using:
Fmax=m(g+amax)
Substituting the values:
Fmax=70(10+2.36868)=70×12.36868≈865.8076 N
Step 5: Calculate the Minimum Force (F_min)
The minimum force exerted on the boy when the platform accelerates downwards can be calculated using:
Fmin=m(g−amax)
Substituting the values:
Fmin=70(10−2.36868)=70×7.63132≈532.1924 N
Final Results
- Maximum Force (F_max) ≈ 865.81 N
- Minimum Force (F_min) ≈ 532.19 N
Summary
The maximum and minimum forces exerted on the boy standing on the vibrating platform are approximately 865.81 N and 532.19 N, respectively.
- The mass of the boy (m) = 70 kg
- The frequency of vibration (f) = 1 vibration per second
- The amplitude of vibration (A) = 6 cm = 0.06 m
- Acceleration due to gravity (g) = 10 m/s² (for simplicity)
The angular frequency (ω) is related to the frequency (f) by the formula:
ω=2πf
Substituting the value of f:
ω=2π×1=2π rad/s
The maximum acceleration in harmonic motion can be calculated using the formula:
amax=Aω2
Substituting the values:
amax=0.06×(2π)2
Calculating (2π)2:
(2π)2≈39.478
Thus,
amax=0.06×39.478≈2.36868 m/s2
The maximum force exerted on the boy when the platform accelerates upwards can be calculated using:
Fmax=m(g+amax)
Substituting the values:
Fmax=70(10+2.36868)=70×12.36868≈865.8076 N
The minimum force exerted on the boy when the platform accelerates downwards can be calculated using:
Fmin=m(g−amax)
Substituting the values:
Fmin=70(10−2.36868)=70×7.63132≈532.1924 N
- Maximum Force (F_max) ≈ 865.81 N
- Minimum Force (F_min) ≈ 532.19 N
The maximum and minimum forces exerted on the boy standing on the vibrating platform are approximately 865.81 N and 532.19 N, respectively.
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:PRACTICE PROBLEMS 2
Explore 20 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Conceptual Questions
Explore 18 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
A man stands on a weighing machin palced on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the readin of the weighing machin? Teh amplitude of vibration of platform is 5cm. Take g=10ms−1
View SolutionWhen a man stands on a weighing machine placed on a horizontal platform, it reads 60 kg . With the help of a suitable mechanism, the platform is made to undergo vertical harmonic vibrations with a frequency of 1 vibration per second. Determine the effect of this S.H.M. on the reading of the weighing machine, The amplitude of vibration of the platform is 4 cm. Take g = 10 m/s2.
View Solution
Knowledge Check
A man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2πHz. Which of the following statement is correct ?
 AThe spring balance reads the weight of man as 60kgBThe spring balance reading fluctuates between 60kg and 70kgCThe spring balance reading fluctuates bettween 50kg and 60kgDThe spring balance reading fluctuates between 50kg and 70kg
AThe spring balance reads the weight of man as 60kgBThe spring balance reading fluctuates between 60kg and 70kgCThe spring balance reading fluctuates bettween 50kg and 60kgDThe spring balance reading fluctuates between 50kg and 70kgA mass of 80kg stands on a horizontal weight machine of negligible mass , attached to a massless platform P that sliding down at 37∘ incline. The weight machine reads 72kg the man is always at rest weight machine calculate

a. the vertical acceleration of the man.
b. the coefficient of kinetic friction μ between platform and incline.A1324B1524C1124D1724Two bodies of masses 1 kg and 4 kg are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency 25 rad s−1, and amplitude 1.6 cm while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take g=10ms−2).
 A20 NB60 NC40 ND10 N
A20 NB60 NC40 ND10 N
The bob of a simple pendulum executes simple harmonic motion with amplitude 4 cm and frequency 10 vibrations per second. Calculate the kinetic energy of the bob in lowest position if mass of bob is 2 kg.
View SolutionA boy is standing on a weighing machine placed on the floor of an elevator. The elevator starts going down with some acceleration, moves with constant velocity for some time and finally decelerates to stop. The minimum and maximum weight recorded are 480N and 840N If the magnitude of reardation is double of acceleration, find (a) true weight of the boy and (b) magnitude of acceleration.
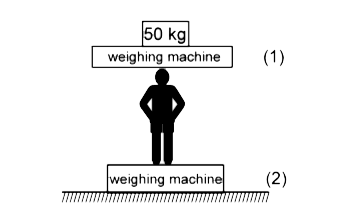
View SolutionA man of mass 60 kg is standing on a weighing machine (2) of mass 5kg placed on ground. Another identical weighing machine is placed over man’s head. A block of mass 50kg is put on the weighing machine (1) . Calculate the readings of weighing machines (1) and (2) .
View SolutionTwo blocks A and B having mass m = 1 kg and M = 4 kg respectively are attached to a spring and placed vertically on a weighing machine as shown in the figure. Block A is held so that the spring is relaxed. A is released from this position and it performs simple harmonic motion with angular frequency w=25rads−1. The spring remains vertical
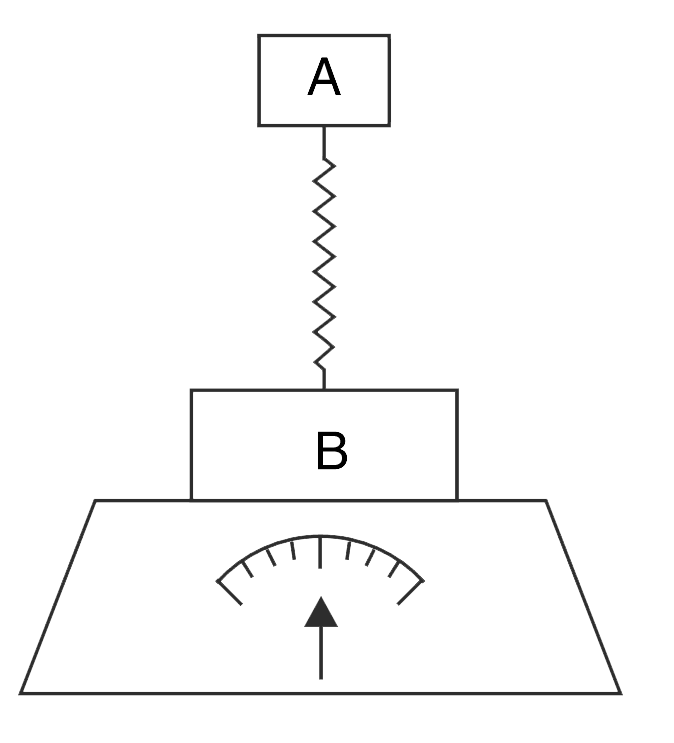
(a) Find the reading of the weighing machine as a function of time. Take t = 0 when A is released.
(b) What is the maximum reading of the weighing machine ?
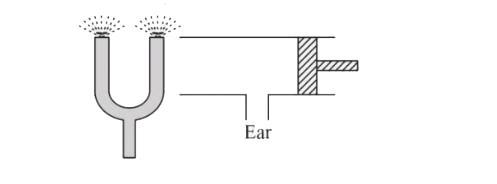
View SolutionA vibrating tuning fork of frequency n is placed near the open end of a long cylindrical tube. The tube has a side opening and is also fitted with a movable reflecting piston. As the piston is moved through 8.75 cm, the intensity of sound just changes from a maximum to minimum. If the speed of sound is
350 metre per second, the value of n is N3 then N is.
View Solution

