A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

2π√2mk
2π√m2k
2π√mk
2π√m2k
The correct Answer is:B
Total restoring force on the mass along OA-
Fnet=FA+FBcos45∘+FCcos45∘
=ky+2ky.cos45∘.
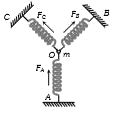
⇒Fnet=ke+2k(ycos45∘)cos45∘=2ky
⇒Fnet=k.y
∴k.=2k, T=2π√mk.=2π√m2k.
Similar Questions
A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionA particle of mass 'm' is attached to three identical springs A, B and C each of force constant 'k' as shown in figure. If the particle of mass 'm' is pushed sightly against the spring 'A' and released. Find the period of oscillation
View SolutionA particle of mass 'm' is attached to three identical springs A, B and C each of force constant 'k' as shown in figure. If the particle of mass 'm' is pushed sightly against the spring 'A' and released. Find the period of oscillation
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA particle of mass m is attached to three identical massless springs of spring constant 'k' as shown in the figure. The time period of vertical oscillation of the particle is

View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
View Solution
