A uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal.
sinθ=12√ρ0/ρ
sinθ=12ρ0ρ
sinθ=√ρ/ρ0
sinθ=ρ0/ρ
The correct Answer is:A
Force of buoyancy-
FB=Alρ0g (l=PR)
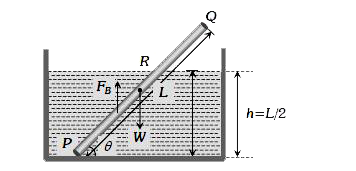
For rotational equilibrium-
Alρ0g×l2cosθ=ALρg×L2cosθ
⇒l2L2=ρρ0⇒lL=√ρρ0
⇒sinθ=hlL2l=12√ρ0ρ.
Similar Questions
A rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
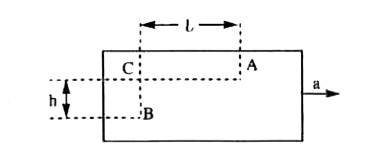
View SolutionA sealed tank containing a liquid of density rho moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA liquid of density rho_0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density rho is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination theta of the rod with the horizontal in equilibrium position is
View SolutionUniform density rho Rod in a wide tank (sigma) Is a fluid of density, is placed where sigma(sigma gt rho) . The depth of fluid in the tank is half the length of the rod. In equilibrium, the lower end of the rod remains on the lower surface of the tank. At this stage, the rod is horizontally theta Makes an angle. Then, sin theta Will be like
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionDensity of a liquid varies with depth as rho=alphah. A small ball of density rho_0 is released from the free surface of the liquid. Then
View Solution
