A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
sin−1(√ρ0ρ)
sin−1(n√ρ0ρ)
sin−1(1n√ρ0ρ)
sin−1(1n√ρρ0)
The correct Answer is:C
Step by step video, text & image solution for A liquid of density rho_0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density rho is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination theta of the rod with the horizontal in equilibrium position is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 2
50 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A wooden plank of length 1m and uniform cross-section is hinged at one end of the bottom of tank as shown in figure. The tank is filled with water upto a height of 0.5m. Find the angle θ that the plank makes with the vertical in the equilibrium position. [Exclude the case thea=0]

View SolutionAB is a uniformly shaped rod of length L and cross sectional are S, but its density varies with distance from one end A of the rod as ρ=px2+c, where p and c are positive constants. Find out the distance of the centre of mass of this rod from the end A.
View Solution
Knowledge Check
A uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal.
Asinθ=12√ρ0/ρBsinθ=12.ρ0ρCsinθ=√ρ0/ρDsinθ=ρ/ρ0Two non-mixing liquids of densities ρ and (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to :
A{1+(n+1)p}ρB{2+(n+1)p}ρC{2+(n−1)p}ρD{1+(n−1)p}ρTwo non-mixing liquids of densities ρ and (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to :
A{1+(n+1)p}ρB{2+(n+1)p}ρC{2+(n−1)p}ρD{1+(n−1)p}ρ
The density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View Solution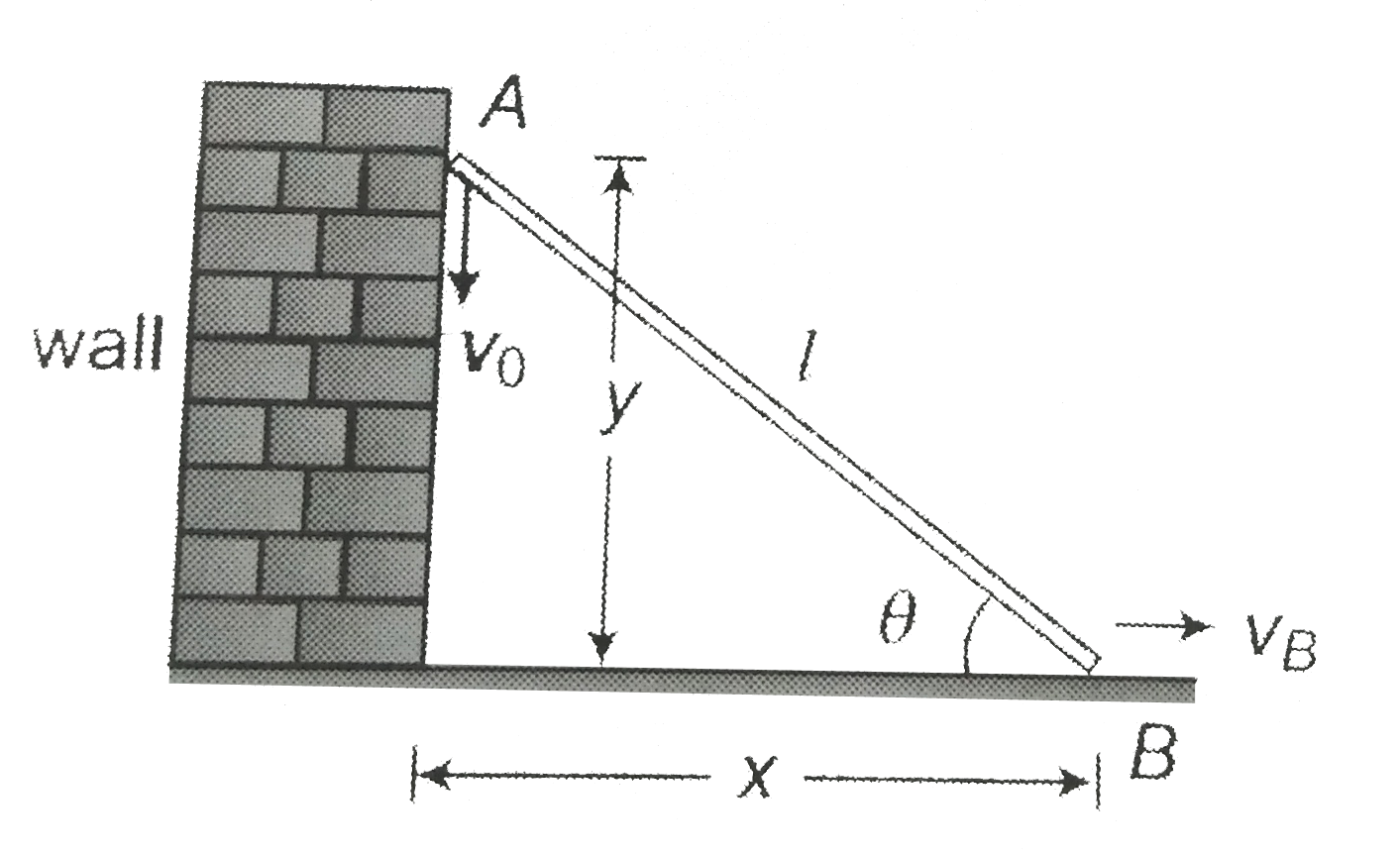
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)

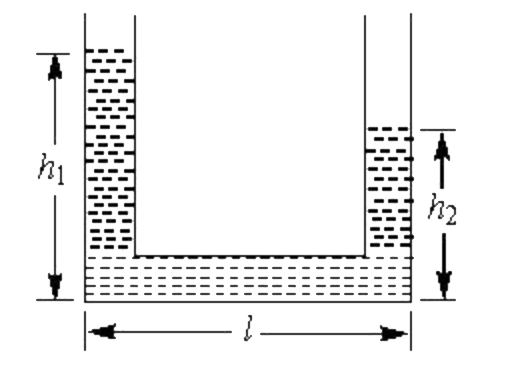
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
View Solution
