Question

The angular momentum of a planet of mass M moving around the sun in an elliptical orbitis $\overrightarrow{L}$. The magnitude of the areal velocity of the planet is :

Options

A. `(4L)/(M)`
B. `(2L)/(M)`
C. `(L)/(M)`
D. `(L)/(2M)`

Answer

D

Explanation

Areal velocity `=(L)/(2m)`
Suppose a planet is revolving around the sun and at any instant its velocity is v, and angle between radius vector `(vecr)` and velocity `(vecv)`. In dt time, it moves by a distance vdt, during this dt time, area swept by the radius vector will be OAB which can be assumed to be a triangle.

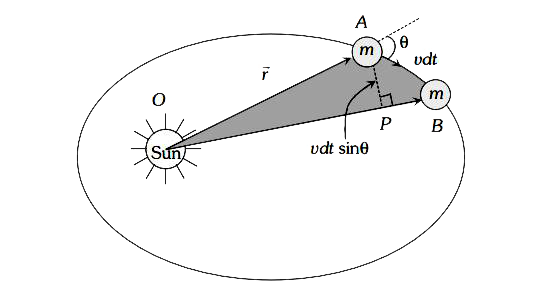
`dA=(1)/(2)` (Base) (Perpendiculr height)
`dA=(1)/(2)(r)(vdt sin theta)`
So, rate of area swept `(dA)/(dt)-(1)/(2)vr sin theta`
we can write `(dA)/(dt)=(1)/(2)(mvr sin theta)/(m)`
where `mvr sin theta` = angular momentum of the planet about the sun, which remains conserved (constant)
`implies (dA)/(dt)="Area velocity"=(L_("planet/sun"))/(2m)=(L)/(2m)`