The areal velocity of the planets revolving around the sun is ………….. .
To find the areal velocity of the planets revolving around the sun, we can follow these steps:
Step 1: Understanding Areal Velocity
Areal velocity is defined as the area swept out by the radius vector of a planet in a given time. According to Kepler's Second Law, the areal velocity of a planet is constant.
Step 2: Define the Area Swept Out
When a planet moves a small angle dθ in a time interval dt, the area dA swept out by the radius vector can be approximated as:
dA=12r2dθ
where r is the distance from the sun to the planet.
Step 3: Relate Areal Velocity to Time
The areal velocity dAdt can be expressed as:
dAdt=12r2dθdt
Here, dθdt is the angular velocity ω.
Step 4: Express Areal Velocity
Substituting ω into the equation, we have:
dAdt=12r2ω
Step 5: Relate Angular Momentum
The angular momentum L of the planet is given by:
L=m⋅r2⋅ω
where m is the mass of the planet.
Step 6: Express Areal Velocity in Terms of Angular Momentum
From the angular momentum equation, we can express ω as:
ω=Lm⋅r2
Substituting this back into the areal velocity equation gives:
dAdt=12r2(Lm⋅r2)=L2m
Step 7: Conclusion
Since the angular momentum L is constant for a planet orbiting the sun, the areal velocity dAdt is also constant. Therefore, the areal velocity of the planets revolving around the sun is constant.
Final Answer
The areal velocity of the planets revolving around the sun is constant.
---
Areal velocity is defined as the area swept out by the radius vector of a planet in a given time. According to Kepler's Second Law, the areal velocity of a planet is constant.
When a planet moves a small angle dθ in a time interval dt, the area dA swept out by the radius vector can be approximated as:
dA=12r2dθ
where r is the distance from the sun to the planet.
The areal velocity dAdt can be expressed as:
dAdt=12r2dθdt
Here, dθdt is the angular velocity ω.
Substituting ω into the equation, we have:
dAdt=12r2ω
The angular momentum L of the planet is given by:
L=m⋅r2⋅ω
where m is the mass of the planet.
From the angular momentum equation, we can express ω as:
ω=Lm⋅r2
Substituting this back into the areal velocity equation gives:
dAdt=12r2(Lm⋅r2)=L2m
Since the angular momentum L is constant for a planet orbiting the sun, the areal velocity dAdt is also constant. Therefore, the areal velocity of the planets revolving around the sun is constant.
The areal velocity of the planets revolving around the sun is constant.
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Short answer type question)
20 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Long Answer Questions)
4 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Additional questions)
5 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Knowledge Check
All the planets move around the sun in
Acircular pathBrectangular pathCelongated elliptical pathDnone of the aboveThe earth revolved around the sun.
Awas revolvingBis revolvingChad revolvedDrevolvesAccording the Kepler's law, the areal velocity of a planet around the sun, always
AincreasesBdecreasesCremains constantDfirst increases and then decreases
A planet revolves about the sun in an elliptical orbit of semi-major axis 2×1012m. The areal velocity of the planet when it is nearest to the sun is 4.4×1016m/s. The least distance between the planet and the sun is 1.8×1012m/s. The minimum speed of the planet in km/s is 10K. determine the value of K.
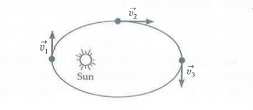
View SolutionFigure shows the velocity of a planet revolving around the sun at three times of a year. Let υ be the speed of the planet when its velocity is →υWhich of the following alternatives is correct?
View SolutionA planet revolves about the sun in an elliptical orbit of semi-major axis 2×1012m. The areal velocity of the planet when it is nearest to the sun is 4.4×1016m/s. The least distance between the planet and the sun is 1.8×1012m/s. The minimum speed of the planet in km/s is 10K. determine the value of K.
View SolutionWhen is KE of a planet revolving around the sunn maximum?
View SolutionAll the planets move around the sun in an _________
View Solution
